一、前言#

        作者意识到，过去的隐私保护策略是以牺牲学习性能为前提的。作者认为产生这个问题的根本原因在于“模型效用”和“数据隐私”之间的关系没有被准确识别，导致隐私约束过于严格。在文中下，作者从最适化的角度来解决这个问题，并将问题描述为：“在给定一组隐私约束的情况下，使得准确性损失最小”。作者使用灵敏度来描述噪声对模型效用的扰动影响，并提出了一种新的优化噪声机制，该机制可以在符合差分隐私约束的前提下，提高整体学习的精确度。

二、介绍#

2.1 论文结构#

        在作者的模型中，作者假设拥有对学习模型的白盒访问权，拥有任意辅助信息，并且隐私机制是公开的。

        主要问题在于：当差分隐私的机制将噪声添加到模型参数中时，随着隐私要求变得严格，学习结果的效用会显著降低，即使使用矩统计已经显著改善了强组合的效用，问题仍旧没有彻底解决。

        作者观察到，模型参数可以在一些精心优化的方向上扰动，从而使模型精度损失最小化。

        因此，作者利用精度损失的近似值，把“设计最适性差分隐私深度学习机制”转化成“优化问题”，该问题搜索扰动噪声的概率密度函数，以最小化差分隐私约束下的加权模型失真。

2.2 前人工作#

• shokri等人的工作，组合方法仍旧需要大量的隐私预算。Abadi等人的方法，在MNIST上只有90%的精度。

• 现有的差分隐私机制大多是启发式的，因为隐私政策过于保守，往往需要添加过多的噪声，这对结果有害。

• 作者没有关注成本的凸性，而是关注算法的实际性能。

• 差分隐私最佳机制证明了当维度d=2和离散查询输出设置时，最佳噪声概率分布具有相关的多维阶梯形pdf（概率密度函数），但结论很难用于作者工作所针对的高维度场景。

三、背景#

        主要介绍了差分隐私和随机梯度下降SGD相关的知识。

        在前两篇文章中已有相关介绍，在此不再赘述。

四、方案#

        在这一节，作者首先抛出了一个发现：参数上的扰动对隐私成本有不同的影响。基于这一点，作者近似了依赖于扰动噪声的效用，并将问题表述为“寻求扰动噪声的概率密度函数”问题，从而使得精度损失最小化。

4.1 模型敏感度#

        首先提出一个问题：对于一个训练模型，如果它的参数都被相同规模的噪声扰动了，那么扰动模型会有相同的精度吗？为了简单化起见，作者使用了成本函数来评估模型的效用：成本越小，效用越高。

        作者做了一个实验，首先创建了一个简单的感知机，输入层为{x1,x2}，隐藏层为{h1,h2}，权重为{θ1,…,θ6}，输出为y。隐藏层使用了sigmoid函数，h1=φ(θ1x1+θ3x2+b1)，y=θ5h1+θ6h2+b3。如图所示：

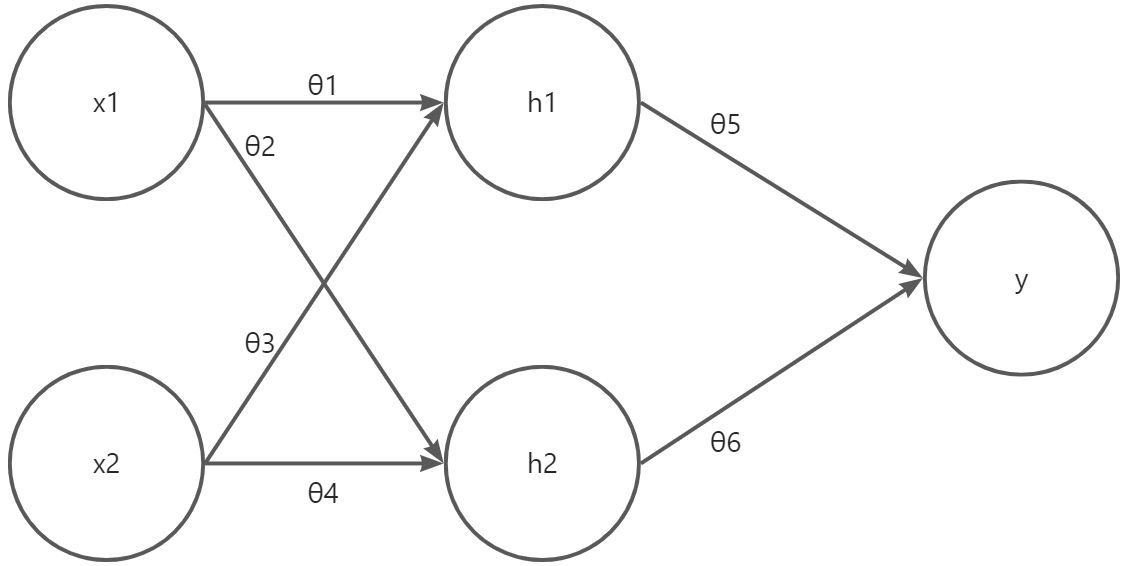
        在对1000个样本进行150回计算后，获得了相关的参数，然后再向其中添加噪声。添加噪声也导致了成本函数关于参数的导数有了区别，由此产生了后面的一系列问题。

作者发现，θ1增加，cost反而减小，这与 $\frac{\partial C}{\partial \theta_1}$ 的正负性保持一致。同理，b3增加时，cost也增加了。

        作者由此得出了结论：成本函数的敏感性在参数空间中是异质的（对各个参数而言都有不同的敏感度变化趋势），导数可以作为敏感性的指标。为了使得成本最小，最好将较高的噪声添加到敏感度较低的参数里，反之亦然。

4.2 问题转化#

        作者向每个裁剪的梯度中增加精心校准后的噪声，添加的噪声是从一个多维的分布中采样的，能够根据他们自身的敏感度，使得整体的扰动成本最小化。

4.2.1 加噪的方向#

        令：$\textbf{w}=(w_1,w_2,...,w_d)\in D^d$ 是所有训练样本成本的导数向量，总共有d个参数，D^{d}表示了可行域。

        加噪的机制为: $K(\textbf{x})=\textbf{x}+\textbf{z},\quad \textbf{z}=(z_1,...,z_d)$ 从一个多维的概率分布P中获得，P将在随后介绍。

        为了使得整体的成本最小化，z应该根据成本函数的最小敏感度方向来选取，而这样的方向是由w来决定的。我们假设目标函数为：

        w表示关于每个参数的模型敏感度。上式的方程可以这样解释：我们将从特定概率分布中提取的随机噪声z投影到由权重w构建的空间上，目标是最小化总投影随机噪声的期望。

        更确切的来说，就是更倾向于把噪声z_i加到那些导数为负的，或者导数尽可能小的方向上去。

4.2.2 P的情况#

        这一部分着重探讨了P应该满足的隐私情况。

        已知，添加的噪声是从一个“由全局敏感度决定的概率分布”中提取的。为了与模型敏感度区分开来，我们使用g^{t}来表示第t次迭代时计算的梯度。

        令$\textbf{g}^t 、\textbf{g’}^t$ 来表示在训练集 X 和 X’ 上计算出来的两个梯度向量。这两个数据集彼此之间只有一个样本的差距。全局敏感度可以表达为：

        根据差分隐私的定义，机制K需要满足如下的条件：

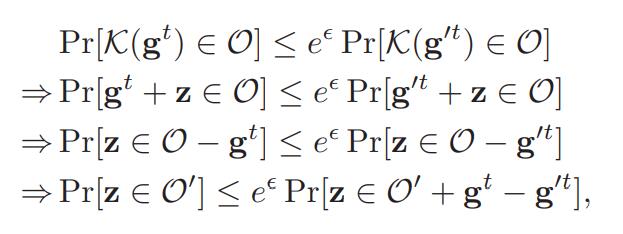
        令$Δ=g^{t}-g'^{t}$，这样上式可以改写成：

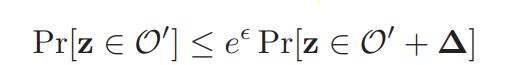
        这样，对于任意的O’和||Δ||＜a,，差分隐私的约束条件就可以转化成P上的概率分布约束。

        我们假设 z 遵循P的概率分布，其概率密度函数为 p(z)。为了满足上式，只需要找到概率密度函数p，当Δ有界时，$ln\frac{p(\textbf{z})}{p(\textbf{z}+\Delta)}$ 也就有界了。

        综上所述，该部分的问题可以总结为以下程式：

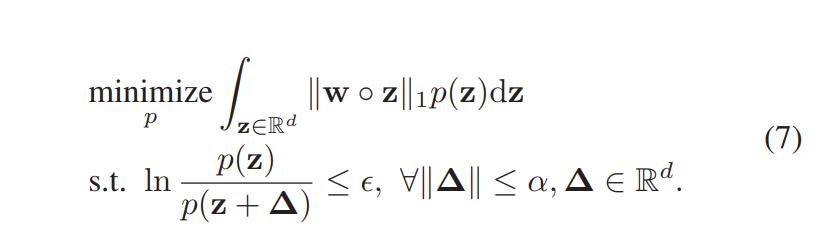
4.3 主要结论#

        为了解决第（7）式，作者首先假设p是一个每个维度互相独立的多元高斯分布，因此我们能够列出它的概率密度函数：$p(\textbf{z})=\prod_{i=1}^{d}p_i(z_i)$，其中，$p_i(z_i)$

是 $N(0,\sigma_i^2)$ 的概率密度函数，随机噪声z_i也是从这里绘制的。问题可以化为：

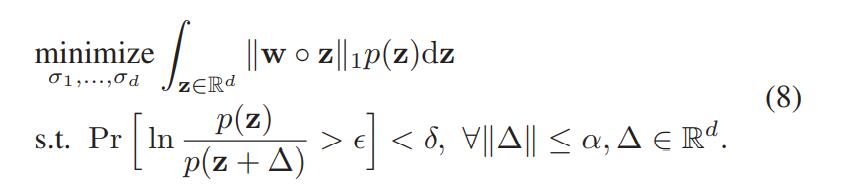
        对上式，把高斯分布的情况代入其中：

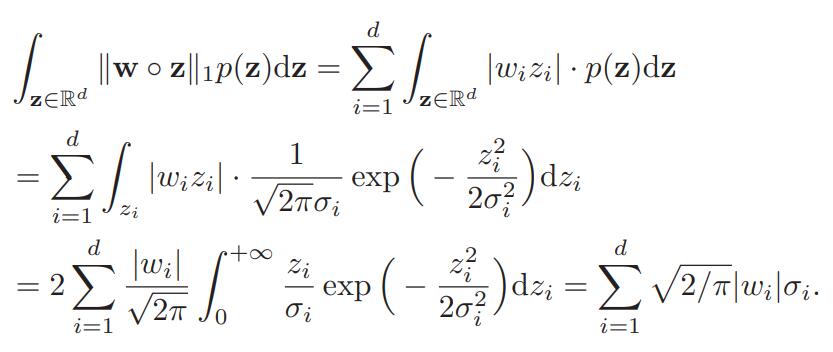
        这样问题就变成了使得σ的权重和 σ=(σ1,…,σd) 最小。

        然后考虑约束条件。根据“矩统计理论”，一个关于隐私损失变量 $c=\ln\frac{p(\textbf z) }{p(\textbf{z}+\Delta)}$ 的高阶矩被应用到了差分隐私约束中。这样的理由是，对c高阶矩的约束能够给出更大的约束变量的可行范围，这有助于找到式(8)的全局最优解。根据马尔可夫不等式：$P(x\geq a)\leq\frac{E(x)}{a}$ ，可以把约束条件变为：

        因为z符合高斯分布，因此可以把含有z的表达式c也写成高斯分布的形式：

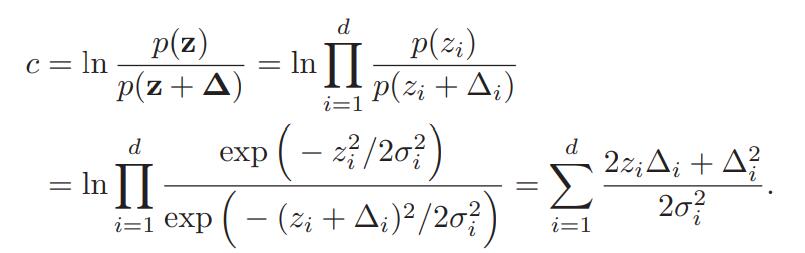
        同时，$z_i\sim N(0,\sigma_i^2)$，因此有：

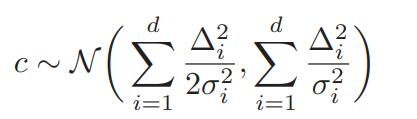
        把c的表达式代入到马尔可夫不等式中：

        解上述不等式：

        把目前为止的推理结果整合起来，令$\tau(\epsilon,\delta)\triangleq2\epsilon+(2/\lambda)ln\delta$ ，那么复杂的式(8)就可以化简为：

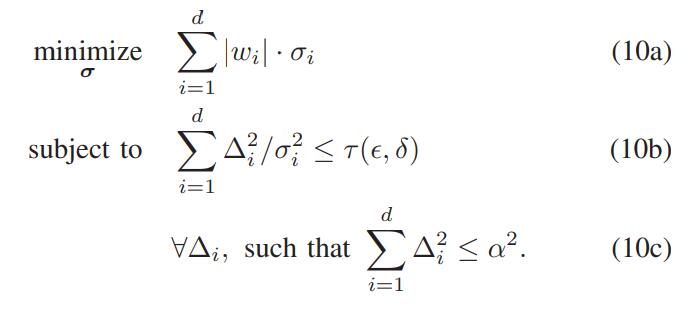
        考虑到等式 $\sum_{i=1}^d\Delta_i^2=a^2$ 不仅符合式(10c)，而且具备更广的应用，因此，式(10）最终可以化为：

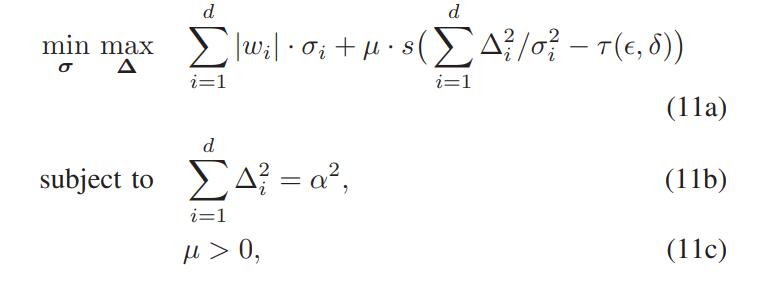
        其中，s(x)是这样的一个函数：当x小于0时u，结果为0；否则为1。作者证明了当μ趋向于+∞时，式10等同于式11。

        作者在不断增加μ的同时，更新σ和Δ的值，使用sigmod函数替代s(x)，使用标准化技术处理非凸问题，每一步向着负梯度的方向逼近参数然后投影到可行域中。

        对于每次更新的参数，作者给出了结论：对于k个迭代器实现(ε，δ)-差分隐私，第t次迭代应该满足（ε^t，δ^t）-差分隐私，即：

4.4 隐私机制#

        算法过程如图所示：

        作者证明了该算法符合差分隐私。

五、评估#

5.1 应用#

        作者使用了投影梯度下降法，在每次迭代中，该下降沿投影到约束集的梯度的相反方向移动，该方法大概需要50次迭代才能收敛。

        在实验的过程中，最大的挑战在于高维度导致的计算时间过长。原因在于基于numpy的最优化和噪声生成并没有有效利用GPU加速。即使提高了高斯噪声生成器的速度，最适化噪声生成器的性能仍旧不理想，这是由于tensor operation在高维分布中随机生成向量是相当低效的。

        因此，最终的噪声生成器分成两个部分：一个tensor计算噪声分布，一个Numpy噪声生成器。

5.2 实验设置#

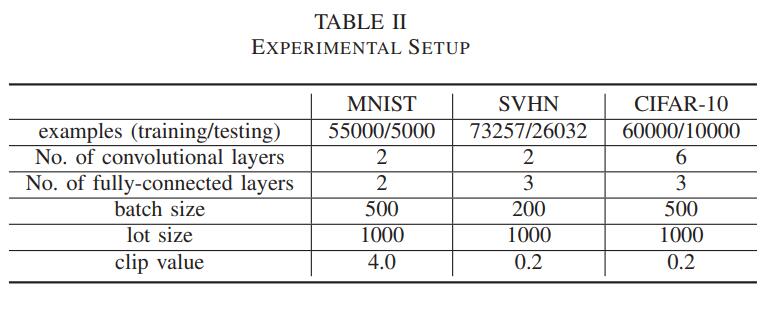
5.3 和矩统计的比较#

        MNIST：优化后的噪声生成器在各个级别上的精确度都高于高斯生成器，在隐私级别更高时结果更加显著。

        SVHN：不论是高隐私要求还是低隐私要求，作者的模型精确度都要比高斯模型的更高。

        CIFAR-10：应对复杂数据集，模型的精确度有所下降，但仍旧比高斯模型的高。

5.4 模型结构的敏感度#

        作者表明，优化机制对模型结构和超参数的变化具有高度鲁棒性。

        考虑以下可能影响结果的超参数：批量大小、隐藏层单元数和l2限幅值α。对于每组实验，重复使用之前的设置，但受控超参数除外。

        直觉上，lot大小越小，模型就需要添加更多的噪声，精确度应该更低。但实际上，更多的噪声并不一定会导致精确度的降低。由于最优化噪声机制谨慎地校准了噪声以使得成本最小化，模型精度受lot规模的影响很小。

        但是，由于本文的思路是围绕着成本函数展开的，主要考察的是沿着梯度下降的方向添加噪声，因此裁剪值的大小会严重影响精确度。当裁剪值很小时，参数的变化受到裁剪的约束，精确度会被影响。

        但是高斯机制并没有这样的表现，因为当裁剪值较大时，添加的噪声太大了。

六、结论#

        在本文中，作者寻求一种优化的差分隐私机制，用于在众包用户数据上执行隐私保护学习。该问题被描述为一个优化，该优化最小化了一组差分隐私约束下的精度损失。问题的高维性是一个主要障碍，因此作者从理论和工程角度解决它。对MNIST、SVHN和CIFAR-10的评估表明，作者提出的隐私机制提高了所有隐私级别的模型准确性，特别是在高隐私制度下，但只增加了可忽略的运行时开销。