一、前言#

        用户的数据如果是从多个来源收集或者多个实体之间互相共享的话，那么用户隐私将会产生很大的问题。这就是“分布式数据分析”，而差分隐私是解决这个问题的一个可能的方向。在此之前的技术存在着诸多的问题：大多支持集中式的数据库，在分布式数据集中容易产生“串通”、需要在隐私和效率之间进行权衡、在交流和计算成本上效率低下……

        作者提出了DstrDP(分布式差分隐私协议)，主要目标是从分布式数据库中生成符合差分隐私规范的集中式结果。作者采用的是拉普拉斯机制，在保持用户数据的最佳效用的前提下、不依赖于任何受信方、且只要解密密钥保持隐秘，就能生成抵抗“串通”的拉普拉斯噪声。作者使用了决策树分类器来作为工具，表明了DstrDP能够保护中间结果的隐私、通过评估性能来确认其效率。

【概念】分布式分析（distributed analysis）、集中式结果（aggregate result）、串通（collusion）、解密密钥（decryption key）

【重点】

• 实验的流程是怎么样的？

• 如何确保流程符合DP规范的？

• 如何实现“隐私”和“效用”的权衡的？

• 实验的性能相比前人的研究有何进步？

二、介绍#

2.1 引入#

        在处理隐私数据时，一共有两种隐私时是值得注意的：

• 计算型隐私：不允许任何实体访问整个数据库的情况下，对隐私数据进行计算

• 输出型隐私：最终结果应该得到保护，因为如果对这些结果进行溯源工作的话很有可能会得到一些具体用户的数据。

        在论文中，作者探究了在“分布式数据集”中使用DP的可能性，这种情况下，需要统合各个互不信任的部分来合作计算它们数据并集的统计数据。

        作者围绕以下两个问题，对“计算型隐私”和“输出型隐私”都进行了实现：

• 如何在不向参与者揭露数据的情况下，查询一个分布式数据集？

• 如何使得查询结果符合差分隐私的规范？

2.2 贡献#

        把DP技术应用到分布式设置上，需要解决一系列的问题，包括：隐私和效用的权衡；低效的；回答污染；串通……

        作者的训练是基于ID-3决策树的。这个DstrDP的优势包含了以下几点：

• 强隐私性：数据所有者从其他人的数据中学习不到任何东西，对于数据集成者而言，只有差分隐私的结果是公开的。

• 反串通（或者“对串通有弹性”）：DstrDP基于了这样一种假设：所有参与进来的组织都有可能互相串通，这里没有可信的群体。这是和其他方法相比一个最根本的区别。其他方法都依赖于“最诚实主体假设”并且串通方能够立即阅读个体的用户数据。

• 最佳效用：计算查询的结果受“符合DP规范的最小噪声总量”影响而扰动，因而作者的方法提供了最佳的效用。

• 效率：对挖掘算法而言，引入的DstrDP的开销是微不足道的。另外，在没有任何重大性能损失的前提下，DstrDP能够支持大量的数据所有者，并且交流的开销和数据持有者的数量呈正比。

        由于同态加密仅对整数起作用，因此还需要解决DP机制会引入实数的问题。此外，在差分隐私基础上构建决策树，阻止算法进一步扩张的分类器因素(classic factors)将不再起作用，这也需要得到解决。

三、背景#

3.1 差分隐私（DP）#

        诸多内容已经在前面三篇中介绍过了，在此仅作简单区分：

• 定义公式：定义中，作者使用的公式为经典公式，也即不包含δ的那版；

• 添加噪声：作者使用的是拉普拉斯噪声；

• 隐私预算：对于查询组合，作者使用的还是最经典的模型，也即：$\sum_{i=1}^{k}\epsilon_i-DP$，没有使用“强组合定理”、“矩统计”或者“RDP”来更紧地限定隐私成本的上界。

• DP数据分析：包括交互式和非交互式。

• 非交互式：由数据持有者对数据进行扰动，然后再发布。

• 交互式下：数据集可以是集中的或者分布式的。

• 集中环境下：数据集成者向远程数据集发出查询，数据持有者对查询结果进行扰动保证DP标准，然后发送给对方；

• 分布式环境：数据集成者查询多方拥有的数据集，并且只能够获得已经添加了噪声的结果。

3.2 安全多方计算（SMC）#

        主要用于以下场景：有多个参与方想要使用他们自己的隐私数据去参与计算一个函数，而又不想要把数据揭露给其他人。

        DstrDP正是一种SMC算法，它对数据集成者甚至是数据所有者（如果有必要的话）只提供了掺杂了噪声的集成结果。

3.3 同态加密（HE）#

        提供同态的密码系统可以在不需要解密密钥的情况下计算加密值。

        在一个公钥加密系统中，对于一个给定的数值x，使用公钥pk加密，结果记为 $[x]_{pk}$ 或者简写为[x]。如果一个密码系统符合：在不知道解密密钥的前提下，能够根据[x]和[y]计算[x+y]，那就说这个加密是“加性同态”。另一个性质是给定[x]和固定的整数c，能够计算[c.x]。假设所有的同态算法都已经模n^2了，并且n^2已被隐藏。

有很多的公钥密码系统是符合这个条件的。作者选取了“Paillier密码系统”。公钥为n，两个私密素数为p和q。简单起见，整数x的加密是通过随机选取整数r然后计算如下式子得到的：

3.4 茫然传输协议（OT）#

        简单来说，1-2 OT里，发射者有两个信息{M0, M1}。接收者有一个选择集合c∈{0，1}。传输结束后，接收者只获得了Mc，并且对另外的信息M（1-c）毫不知情，发送者对c也不知情。1-2 OT 可以泛化为 1-n OT，这种情况下，信息集合为{M1, M2,…, M(N-1)}，选择值为{0,…,N-1}。

        另外还有一种比较冷门的OT：A发送一个信息，B有1/2的概率接收到信息。发送结束后，A不知道B有没有接收到信息，但B直到自己是否接收到了信息。

四、问题陈述#

4.1 问题设置#

        在分布式环境下，一个集成者希望能够向数据集查询以获得差分隐私的集成结果。集成者发出了诸多的统计查询，因此决策树在集成者端构建。

4.2 隐私目标#

        一共有两种“统计查询”（count queries）：

• 每个数据所有者的计数统计，作者使用了“同态加密”（HE）来保护个人隐私。

• 这些计数的累加，作者使用了差分隐私技术来保证输出隐私。

4.3 威胁模型#

        DstrDP基于“semi-honest”攻击模型，也就是“半诚实”模型。在这个模型下，所有的参与方都会遵守协议的执行，但有可能会保留协议的中间状态。攻击者既可能是集成者，也可能是其中一个数据持有者。

        另一方面，还存在“恶意攻击者”模型，攻击者可以通过更改输入来任意地偏离协议规范。

        DstrDP协议里，只有集成者直到查询的结果，数据持有者只能访问数据的加密值，而不能推测出任何明文信息。除此以外，只要集成者的私钥还是隐秘的，那么DstrDP协议就能够防止恶意的数据持有者进行串通攻击。

五、DstrDP 协议#

5.1 相关介绍#

• 基于安全累加（secure sum）的分布式ID3决策树：由集成者向各个数据集查询，使用安全累加协议来保护个体隐私。然而组成个体计数隐私的集成计数(aggregator count)暴露给了集成者。

• 使用SuLQ协议的分布式ID3决策树：主要用于集中的数据集，数据持有者向各自的计数里添加噪声，然后把这些符合差分隐私标准的数据发送给集成者。但这样会剧烈地影响效用。集成计数将会有一个标准差为 $\sqrt{N}$ 的噪声，与目标（单个噪声实现DP，隐私和实用性之间保持权衡）不符。

• 使用SDQ协议的ID3决策树：结合安全计数协议和差分隐私，在集成计数上保持相同等级的差分隐私标准。第一种方法里，存在一个受信任的数据持有者，在执行secure sum协议之前往数据集里添加噪声。第二种方法里，所有数据所有者共同随机选择一方添加噪声。第一种方法，受信方会被全体参与者知晓，因此集成者可以通过破坏受信方并获取噪声，从而逆向破解保护。第二种方法依赖于secure sum，这对合谋攻击不起作用。

5.2 提出的方法#

        计算型隐私通过“同态加密”保护；输出型隐私通过添加拉普拉斯噪声来保证差分隐私的标准规范。作者设计了一个“随机选择协议”来随机且安全地选择一个实现了DP保护的数据持有者。

        简单来说，一个数据持有者给每个其他的持有者分发了一个独立不重合的标识i∈[0,N-1]，集成者选择了一个随机的值R∈[0，N-1]，并且按照如下规则生成了N条信息：

• Mi=1，如果i-R=0 mod N

• Mi=0，其他

        记标识符为i的持有者接收到的信息为Mi。在流程结束的时候，数据持有者接收到信息为1的，将会生成拉普拉斯噪声。这样，除了被选中的个体之外，没有人直到谁被选中了。当然了，标识符不能够泄露给集成者，不然一切都没意义了。

        整体的步骤如下所示：

1. 数据持有者和集成者共同执行随机选择协议，选择Pi作为噪声生成者

2. 每个数据持有者从他的数据集中提取单个计数di，在集成者的公钥下加密为 [di]，加密信息传递给下一个人，接收者也这样提取数据、加密，然后同态相加。

3. 到添加噪声的人时，把自己的数据加入拉普拉斯噪声，然后同态加密

4. 最后的那个人通过添加dp噪声，把数据传给集成者。

5. 集成者解密，然后获得了符合差分隐私规范的数据。

5.3 相关分析#

• 安全分析

    - 【引理1】Pi方的独立计数di不会泄露

    - 【证明1】每个参与方通过公钥进行加密，然后传递信息，只要公钥没有泄露出去，那么监听者就不能窃取数据。

    - 【引理2】准确的集成计数既不会显示给集成者，也不会显示给用户。

    - 【证明2】如果攻击者是集成者，那么他只能得到添加了噪声的数据；如果他是用户，他什么也不会得到。

• 组合分析：在Paillier加密体系下，每个数据所有者以n^2比特的长度给下一个数据持有者提供加密值，交互次数等于数据持有者数量N，因此通信带宽为N×n^2位。

六、基于ID3的DstrDP#

6.1 算法思路#

        输入是一组数据记录D，属性集R和类属性C。

        ID3算法使用贪心策略构建决策树。首先，根保存所有记录。然后，选择具有最大信息增益或最小熵的属性，并根据所选属性的值对记录进行分区。在每个分区上递归地应用相同的过程，直到没有进一步的拆分来改进分类。

        如果满足这三个条件之一，递归函数将停止： 1）没有更多的数据记录进行拆分，2）所有或大部分数据记录具有相同的类标签，3）属性集R为空。

        选择熵最小的属性作为分裂属性。因此，构建差分隐私决策树的问题可以简化为计算差分隐私熵函数的问题。

        熵函数为：

6.2 交流复杂度#

        基于熵函数，DstrDP 协议应针对每个属性执行 m×(l+1) 次。其中 m 是每个属性采用的可能值的数量，l 显示类属性采用的值的数量。因为有 |R|个数据库中的属性数量，DstrDP 协议应在每个节点执行 O(m × l × |R|) 次。

        如前所述，DstrDP 协议的通信带宽为 N × n2 位。因此，差分隐私分布式 ID3 算法在每个节点的通信是 O(m × l × |R|×N × n2)。这种复杂性乘以节点数量将显示总通信带宽。

七、表现评估#

7.1 应用#

        使用java实现，从分布式数据集构建决策树，参与者使用sockets交流。

• 停止标准：由于引入了噪声，因此第一个停止标准不再适用（没有更多的数据记录可供拆分，因为噪声不属于整数，切割实数导致标准不再一致）。

        聚合器生成一个随机值 R 并将其与计数查询一起发送给第一个数据所有者。如果数据所有者的个人计数为 0，则他保持 R 不变，否则，他将随机值添加到 R。他将结果传递给下一个数据所有者。此过程在所有数据所有者中继续进行，然后集成者接收加密的集成计数以及随机值。

        集成者识别接收到的随机值是否等于 R。如果是这样，则意味着准确集成计数的值为 0，应该停止 ID3 算法。

        由于所有人是一个环形的交流状态，如果两个相邻的人串通的话，他们可以很容易地了解其个人计数是否为零。考虑到协议提供的效率和可扩展性属性，作者认为这些类型的信息泄漏是可以接受的。

        当满足第一个标准并且剩余的隐私预算允许聚合器应用更多查询时，此技术很有用。这意味着，在大多数情况下不需要使用这种技术，因为隐私预算已经限制了发出更多查询的算法。

• 过拟合：为了避免过拟合，于是对树深进行了限制

• 实值问题：由于拉普拉斯噪声是实数，因而对于同态加密的整数要求不满足。直接四舍五入，又太过粗糙了。因而作者把所有的值都乘以1000，然后再取邻近实值，这样得到的结果就相对精确了。

7.2 实验设置#

        使用了如下的数据集：

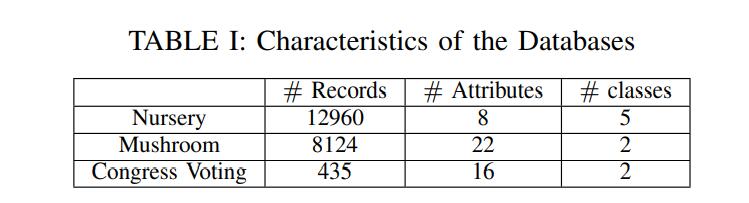
        作者使用了 75% 的记录作为训练数据，25% 作为测试数据。通过改变隐私成本(ε ) 在分布式数据上构建深度高达 7 的决策树，然后测量决策树的准确性。作者使用了 1024-Paillier 加密密码系统进行了实验。

7.3 实验结果#

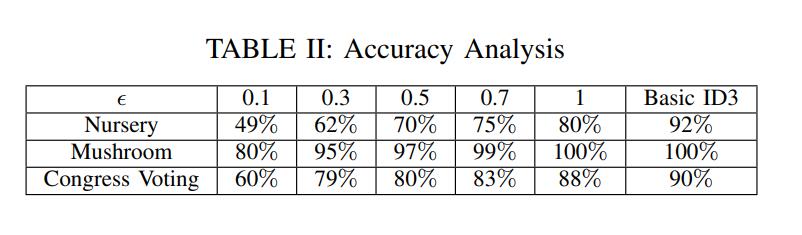
        ε越大，精确度越高。因为这意味着隐私要求越松，添加的噪声可以越小。

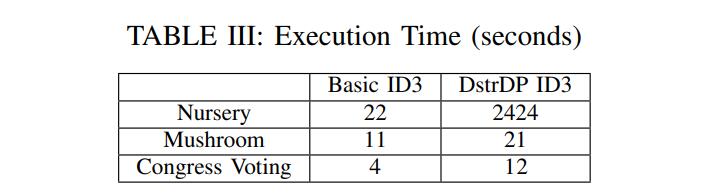
        DstrDP 协议只需要大约 60 毫秒来执行一个计数查询，而最近关于差分隐私的工作需要执行拉普拉斯机制大约需要 15.5 秒。这使得作者的协议适用于数据挖掘算法。

八、相关工作和总结#

        DstrDP 提供了最佳的数据效用，因为聚合计数仅受到一个 DP 噪声的干扰。 DstrDP 不假定任何一方是受信任的。作者实现了 DstrDP 协议，进行了性能评估并展示了它在分布式数据分析中的实用性。 DstrDP 可以支持大量数据所有者，而不会造成任何显着的性能损失。作者希望将协议扩展到其他数据挖掘算法，并使用更高效的同态加密密码系统。

九、评价#

9.1 整理#

        针对计算型隐私和输出型隐私都做了保护工作。

        前者，通过设计随机选择算法+同态加密完成保护工作。因为中途还添加了拉普拉斯噪声，而同态加密仅对整数适用，因此作者把所有的数据（包括噪声）都乘以1000，然后进行取整操作。

        后者，通过对随机选择者和流程的最后一人添加噪声，使得整体的隐私成本要求可以更加严格。

9.2 一些和其他方案的区别：#

• 采用的是拉普拉斯噪声而非高斯噪声，因而在差分隐私定义上遵循的也是严格的ε-DP，而非高斯机制下的(ε，δ)-DP。

• 使用随机选择算法，由算法随机指定一人(且只有他自己知道)添加噪声，避免了全部添加噪声造成的巨大隐私成本和精确度下降

• 采用同态加密，安全性相比secure sum更高，即使发生了串联，对方也不知道数据内容。

• 本质是介于secure sum和SuLQ之间，既不是直接公开，也不是全部添加噪声，而是随机选择一人添加噪声，再对集成结果添加噪声。并且把SDQ的secure sum换成了HE。

9.3 不足之处#

• 对于“恶意攻击者”的威胁模型缺少探讨，只能针对“半诚实”的威胁模型。所有的前提都基于集成者不泄露私钥的前提下。

• 组合定理过于宽泛，基于的是最基本的组合定理。如果能够使用强组合、矩统计或者RDP组合定理，精确度还能进一步提高

• 在构建决策树时，基本上只有自己结果的对比，缺少和其他方案成果的对比