一、前言#

        作者在本文提出了一种新型的安全数据集成框架，名为DPAFT，具备了差分隐私标准和容错度。同时，受Diffie-Hellman密钥交换协议的启发，作者为数据集成提出了一种巧妙的约束关系。在这种关系下，DPAFT能够灵活支持故障容错。

        此外，DPAFT还具备了抵抗差分攻击的能力，通过改进Boneh-Goh-Nissim加密系统使其具备更广泛的适用性。作者还进一步评估了DPAFT的性能，来说明其在存储成本、计算复杂度、差分隐私效用、容错度的鲁棒性以及用户增减效率等方面均有良好表现。

【概念】Diffie-Hellman密钥交换协议，Boneh-Goh-Nissim加密系统

【关注】

• 相关密码协议的阐述及其改进措施、评估方法

• DPAFT模型的性能评估和比较

• 抵抗能力、容错度的证明和验证

二、介绍#

2.1 背景介绍#

        在智能电网系统中，用户家中所有的数据都会连接到一个中心元件——智能电表里面，它会定期收集电器的耗电量并将其报告给本地网关GW，网关将数据集成再转发给CC做进一步的分析和处理，比如做出实时电力定价决策、检测电力欺诈或者泄露。

        但是，实时地使用数据，这里面会包含不少用户的用电模型，与用户的隐私高度相关，因此需要对其进行隐私保护。

2.2 前人工作#

• **大部分方案使用了“同态加密”技术，**这样对于“半信任模型”下的集成器GW，就可以做到在不解密的前提下收集用户的数据。但如果考虑“honest but curious”模型的话，对于持有公钥的CC而言，它将不仅能集成用户数据，而且可以揭露任何用户的使用情况。

• 有一些方案采用了微妙的密钥管理技术，这种方案里，所有的公钥加起来结果为0，以此来将CC的能力去中心化，从而保护数据集成协议的安全性。但该问题对稳定性有很高的要求，不具备容错率。如果有一个用户没有提交，那么整个协议都将失效。毕竟智能电表，作为一种低成本的、在无保护环境下运作的电器，是很容易出错的。

• 差分攻击也是一个重要的问题。现有的问题，要么不具备容错度，要么具备容错度，但效率低、不满足效用和精确度的要求。因此，设计一个高效的、能够保护隐私的、高精度的、具备差分隐私标准、具备容错度的方案是相当重要的。

2.3 本文工作#

• 不同于常规的“严格密钥”($\sum_{i=0}^{n}s_i=0$)方式，本文受 Diffie–Hellman 密钥交换协议的启发，设计了具备如下容错度的密钥计算方式：$s_0·\sum_{i=1}^n(s_i)=1$，其中s_0是CC的私钥；s_i是其余使用者的私钥。

• 使用差分隐私标准来防止用户数据遭受差分攻击。添加的噪声为拉普拉斯噪声。

• 改进了基本的 Boneh-Goh-Nissim 密码系统。隐藏了在 Boneh-Goh-Nissim 密码系统中对于CC来说的私钥 p, 同时引入了对 GW 来说的盲因子 t 和对 CC 的私钥 k, 保护了用户的用电隐私。在“honest-but-curious”的模型中，即只有所有参与者都遵守协议并使用他们各自的秘密信息协同执行程序，才能恢复总使用数据。

三、问题模型#

3.1 系统模型#

一共包含了四类型主体：①受信主体；②控制中心；③网关；④相关用户

• 受信主体（TA）：TA是一个可信任的主体，能够拥有管理整个系统的权限，但并不直接参与流程，直到在汇报中发生了一些意外情况。

• 控制中心（CC）：CC是一个信任度较高的实体，主要职责为收集、处理、分析实时的数据

• 住宅网关（GW）：连接控制中心和住宅用户。主要职责包括“集成”和“中继”，前者把居民区的测量数据集成为一个统一的整体，后者以一个安全的方式协助转发用户和CC之间的交流。

• 住宅用户（U={U_i for i in range(n)}）：通过智能电表、网关，向控制中心每隔15分钟传输一次数据。智能电表可能会出现故障。

3.2 攻击模型#

一共考虑了三种攻击形式：

• 外部攻击：窃听“U-GW”和“GW-CC”的数据

• 内部攻击：攻击者在内部，包括CC、GW这些能够接触到用户数据的主体，甚至是那些寻找其他用户数据的可疑用户

• 恶意软件攻击：攻击者向GW和CC发布了一些难以检测到的恶意软件

对于外部攻击，可以使用同态加密解决。

对于内部攻击，主要考虑“honest-but-curious”攻击模型，例如半诚实模型。这种模型下，用户们都遵守协议的流程，但是通过保留其他用户的输入和中间计算，他们会尽可能地寻找其他用户的信息。

除此以外，还得考虑智能电表的故障损耗等问题。

对隐私以外的攻击超出了本文的分析范畴。

3.3 设计目标#

• 隐私保护：

• 外来攻击者无法通过窃听来揭露用户的隐私数据

• 外来攻击者无法通过向CC和GW安装难以探测的恶意软件来窃取用户数据

• 任何的用户无法通过“窃听或分析所有的输入、中继计算、输出”来推测出其他用户的数据

• 外来攻击者无法通过差分攻击来获取单个用户的隐私

• 容错度：能够在电表发生故障的情况下，继续高效准确地汇总数据。

• 计算效率：计算效率能够支持成千上万的住宅用户的数据集成

四、前置知识#

4.1 Boneh–Goh–Nissim 加密协议#

主要包括了三个算法

• 密钥生成：给定安全参数 τ ∈ Z+，执行 ζ(τ ) 得到元组 (p, q, G)，其中 p, q 是不同的素数，|p| = |q| = τ ，而 G 是 N = pq 阶的循环群。随机选择两个生成器 g, x ∈ G 并设置 $h=x^q$ 。那么，h 是 G 的子群 p 阶的随机生成器。最终，公钥和私钥分别为 PK = (N, G, g, h) 和 SK = p。

• 信息加密：给定消息集合 m ∈ {0, 1,…,V }，其中 V << q 是消息空间的边界，选择一个随机数 r ∈ Z_N，则密文可以计算为 $C=g^mh^r\in G$.

• 信息解密：给定私钥 SK = p 和密文 C ∈ G，首先计算 $C^p=(g^mh^r)^p=(g^p)^m$。令 $g_p=g^p$ ，然后 $C^p=g_p^m$。为了恢复 m，结果将归结为计算 $g_p^m$ 的离散对数。

请注意，当 m 是一条短消息时，例如对于某个小边界 V，m ≤ V，使用 Pollard 的 lambda 方法 ，解密需要预期的时间为O( √ V)。 Boneh-Goh-Nissim 密码系统具有加性同态属性。假设 C1, C2 ∈ G 分别是消息 m1, m2 ∈ {0, 1,…,V } 的两个密文，为了得到 m1 + m2 的密文，可以简单地计算乘积$C=C_1C_2h^r$，其中 r 为一个随机自然数 。

4.2 差分隐私#

具体内容前面几篇已经介绍过，再次不再赘述。本部分主要介绍和拉普拉斯机制相关的内容。

• 由于使用的是拉普拉斯机制，因而差分隐私定义为严格的 (ε)-DP模式。

• 在作者的方案中，假设电表的个数为n，每个电表记为i，用户在汇报信息m_i之前，先把G1(n, λ)-G2(n, λ)的独立同分布添加进去，这样汇报的数据就变成了：

五、基础DPAFT模型#

5.1 系统初始化#

        首先，给定安全参数τ，TA执行函数  ζ(τ )  ，获得元组(p,q,G)

        然后，TA构建 Boneh-Goh-Nissim 加密机制，获得元组(N,G,g,h)，其中N=pq, g∈G为G的一个随机生成器，$h=g^{q\beta}$ 是G的p阶子群的随机生成器

        最后，TA发布(N,G,g,h)作为系统的公钥

        除此以外，系统执行下列步骤，由TA完成密钥材料：

1. 对每个用户U_i，TA随机选择一个自然数s_i，作为U_i的私钥

2. TA计算出自然数s_0，使得 $s_0·(s_1+s_2+...+s_n)=1\space mod \space p$

3. TA把s_0作为 CC 的私钥

4. 对每个s_i，计算 $Y_i=h^{s_0s_i}$，然后把Y_i也作为CC的私钥

5.2 数据集成需求#

        在 t 时刻，CC 向 RA 根据如下步骤发送一个额收集使用数据的请求：

1. CC随机选择一个自然数r，然后计算 $A_1=g^r \space \& \space A_2=h^{s_0r}$

2. CC把A1和A2发送给GW

5.3 数据集成需求中继#

        在接收到A1和A2之后，GW执行如下步骤来完成中继数据集成的请求：

1. GW随机选择一个自然数，然后计算 $A_3=A_1^t=g^{rt}\space \& \space A_4=A_2^t=h^{s_0rt}$

2. GW把A3和A4发给每一个U_i

5.4 用户报告生成#

        每个用户都在时间 t 收集他的使用数据 m_i，然后执行以下步骤：

1. U_i 首先计算使用数据m_i的加密，这个过程用到了U_i的私钥s_i：$C_i=A_3^{m_i}A_4^{s_i}=g^{rtm_i}h^{rts_0s_i}$

2. U_i 把C_i向GW汇报

5.5 隐私保护报告集成#

        如果所有的n个智能电表都正常工作的话，在受到了n个加密数据C_i之后，GW执行如下的步骤来汇报隐私保护报告集成：

1. GW首先集成收集的密文C_i：

1. GW把信息C_γ1发送给CC

        注意到如果存在电表故障、没有发送数据的用户U_i，我们把这个群体算作集合 $\hat{U}$，那么:

1. GW的集成结果将变为：

1. GW把 $\hat{C_\gamma}\space \&\space \hat{U}$ 发送给CC

5.6 安全报告阅读#

        如果n个智能电表都正常工作，在从GW接收到C_γ1后，CC执行以下步骤来解码：

1. CC计算 $C_{\gamma1}h^{-r}=g^{r\sum_{i=1}^nm_i}=\hat{g}^{\sum_{i=1}^nm_i}$，其中 $\hat{g}=g^r$

2. 使用 Pollard 的 lambda 方法，可以在 $O(\sqrt{nW})$ 时间内，通过计算上述值的对数，来获得 $M_{sum}=\sum_{i=1}^nm_i$

        注意到如果有 $\hat{U}$ 集合的电表没有工作，那么CC来执行以下步骤来获得集成数据：

1. 计算 $\overline{C_\gamma}=\Pi_{U_i\in \hat{U}}Y_i=h^{s_0\sum_{U_i\in \hat{U}}s_i}$

2. 计算 $C_\gamma=\hat{C_\gamma}(\overline{C_\gamma})^r=g^{r\sum_{U_i\in U/\hat{U}}m_i}h^r$

3. 重复跟第一种相似的步骤，就可以获得集成数据 $\sum_{U_i\in U/\hat{U}}m_i$

六、增强型DPAFT#

        尽管通过加密方式保护了数据不被泄露，但是通过差分攻击的方式，用户的数据仍旧可以被攻击者掌握。

        在增强型DPAFT中，噪声被添加到个体测量中并由每个住宅用户加密，使得GW只能获得噪声加密的数据。具体来说，受拉普拉斯分布无限可分思想的启发，每个用户 i 在随机选择合适的噪声后，通过简单地先对加密噪声进行积分来扰动智能电表数据。然后，如果某些智能电表不能正常工作，GW 会补充故障智能电表的噪音。最终，通过所有智能电表和GW的分布式协作，实现ε-差分隐私。

6.1 用户报告生成#

        每个用户收集了自己的数据m_i之后，进行如下步骤：

1. 每个U_i首先计算如下的值：$\tilde{C_i}=A_3^{m_i+G_1(n,\lambda)-G_2(n,\lambda)}A_4^{s_i}=g^{rt(m_i+G_1(n,\lambda)-G_2(n,\lambda)}h^{rts_0s_i}$，其中G1和G2是两个从相同的伽马分布中采样得到的随机值。这个伽马分布的概率密度函数为：$g(x,n,\lambda)=\frac{1/\lambda^{1/n}}{\Gamma(1/n)}x^{1/n-1}$

2. U_i向GW汇报这个值

6.2 隐私保护报告集成#

        如果n个智能电表都正常工作，那么在接收到n个$\tilde{C_i}$之后，GW执行如下步骤：

1. 集成计算: $\begin{aligned} \tilde{C_{\gamma 1}}&=(\Pi_{i=1}^b\tilde{C_i})^{t^{-1}}=(g^{r\sum_{i=1}^n(m_i+G_1(n,\lambda)-G_2(n,\lambda))}h^{rs_0\sum_{i=1}^ns_i})^{tt^{-1}}=g^{r\sum_{i=1}^nm_i+Lap(\lambda)}h^r \end{aligned}$

2. 把上式值发给CC

        如果存在集合 $\hat{U}$ 的电表没有正常工作，那么GW将执行以下的工作：

• 先把收集到的数据进行集成计算：

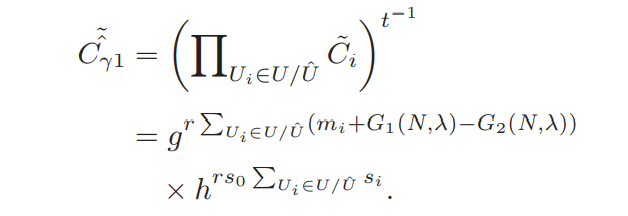
• 再把m个故障智能电表的噪声也添加进来：

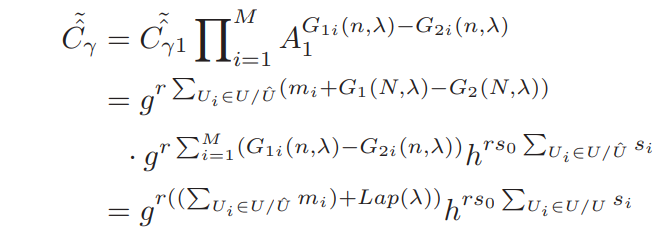
• GW把2中的值和 $\hat{U}$ 发给CC

6.3 安全报告阅读#

        如果n个电表都正常运作，那么CC的处理和五里面的没有什么不同，唯一的区别在于CC得到的输出不再是一个精确值，而是一个附带了拉普拉斯噪声的、符合差分隐私定义的值。

        如果是第二种情况，也即存在集合 $\hat{U}$ 的电表没有正常工作，那么CC将执行以下的工作：

1. 计算 $\overline{C_\gamma}=\Pi_{U_i\in \hat{U}}Y_i=h^{s_0\sum_{U_i\in \hat{U}}s_i}$

2. 计算

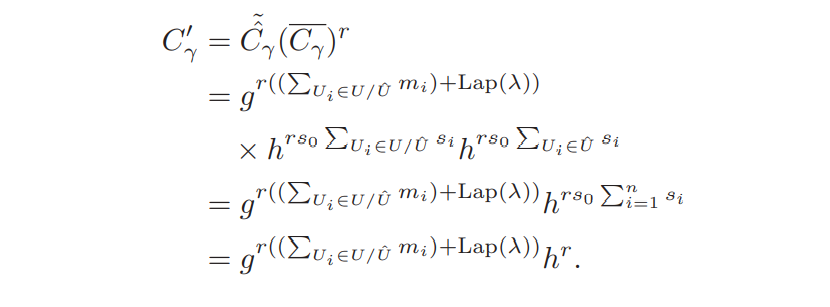
3. 重复跟第一种相似的步骤，就可以获得集成数据 $\sum_{U_i\in U/\hat{U}}m_i+Lap(\lambda)$

七、安全分析#

7.1 防窃听攻击#

        假设攻击者能够对“U-GW”进行窃听，并且得到了一些值，例如：$C_i=A_3^{m_i}A_4^{s_i}=g^{rtm_i}h^{rts_0s_i}$。攻击者可能会通过穷举m_i的每个值来暴力破解，但只要用户的私钥s_i没有泄露，BGN加密系统就能够防止暴力破解攻击。

        同理，集成密文 $C_{\gamma1}=g^{r\sum_{i=1}^nm_i}h^{r}$ 与单用户密文 $C_i=A_3^{m_i}A_4^{s_i}=g^{rtm_i}h^{rts_0s_i}$ 的形式相同，因为值 r 由 CC 秘密保存，所以攻击者 A 在从 GW 到 CC 的通信流 Cγ1监听后也无法获得r，同样无法获得所有用户使用数据的总和 $\sum_{i=1}^nm_i$，更不用说每个用户的使用数据 mi 。

        最后，由于同样的原因，当一些智能电表，比如 $\hat{U}\in U$ 出现故障时，除了CC之外，任何人都无法恢复正常运行的用户使用数据 $\sum_{U_i\in U/\hat{U}}s_i$ 之和，更不用说每个用户的私人使用数据 mi, 即使$\hat{C_\gamma}=(\Pi_{U_i\in U/\hat{U}}C_i)^{t^{-1}}=g^{r\sum_{U_i\in U/\hat{U}}m_i}h^{rs_0\sum_{U_i\in U/\hat{U}}s_i}$和 $\hat{U}$的通信流被窃听.

7.2 防恶意软件攻击#

        如果攻击者向GW的设备进行攻击，获取到了一些数据，但由于GW全程没有做任何解密工作，因此攻击者无法获得任何有效信息。

        如果攻击者向CC的设备进行攻击，他也确实能够获得解密的数据，但那些都是用户的集成数据而非个人数据，个人用户的隐私得到了有效保护。

7.3 防“诚实但好奇”模型的攻击#

        有两种可能的攻击方式。一种是“U-GW”的通信流，被CC内部或者其他住宅用户故意窃听，或者不当保存。另外一种是从“GW-CC”的通信流，被住宅用户的内部参与者窃听。

        前者，由于住宅用户的私钥并没有泄露给其他任何人，因此好奇者并不能从密文$C_i=A_3^{m_i}A_4^{s_i}=g^{rtm_i}h^{rts_0s_i}$ 中解密获得m_i。

        后者，我们发现想要解密中间的信息，必须得有CC的私钥r，否则无法解密用户数据的总和，更不用说单个用户的数据mi了。当一些电表无法汇报值时，由于同样的原因，除了CC之外其他的参与者也无法检索到正常用户使用数据的总和。

7.4 容错的可靠性和安全性#

        经过上面的分析，我们不难发现，如果CC掌握了私钥Y_i，那么就算有 $\hat{U}$ 的用户没有正常上传数据，CC仍旧可以获得正常上传的用户数据总和 $\sum_{U_i\in U/\hat{U}}m_i$。

        由于Y_i和r是CC的私钥，没有它们，任何其他人都不能够解密用户数据的总和，更不用说获得个人用户的信息了。

7.5 防差分隐私攻击#

        根据拉普拉斯无限可分定理，将符合 ε-DP 的拉普拉斯机制拆分成数个伽马分布的机制，然后分别添加给每个用户。这样，即使攻击者能够解密用户的集成数据，也无法应用差分攻击来获得具体的个人隐私。

八、效用评估#

        对比 state-of-the-art schemes  方案。

8.1 存储成本#

• scheme[23]：需要在GW处有大量的缓存来存储“未来密文”

• DPAFT：网关仅负责转发信息，不涉及存储需求

8.2 计算复杂度#

• scheme[23] ：每个用户应该选择其他k个用户作为伙伴来加密测量。具体来说，在他们方案的初始设置阶段，伙伴对每两个用户之间的共享密钥应该是秘密生成和分配的。然后，在数据报告阶段，需要计算并报告两部分密文，即当前密文和未来密文。每个用户通过将随机数和噪声信息添加到实际测量中来生成当前密文。随机数是使用初始设置阶段分配的共享密钥和报告时间点信息计算得出的。然后，还应该同时生成和报告未来的密文，以实现容错。

• DPAFT：无需计算和分配用户之间的共享密钥。未来密文的额外计算也不是必需的。 DPAFT 只需要两次幂运算和一次乘法运算即可报告每个用户的测量结果。计算复杂度小于或至少不比上面的方案大。另外，在honest-but-curious模型中，前者缺乏安全的构建，而本文具备安全模型。

8.3 差分隐私效用#

         2000户家庭，ε设置为1，全局灵敏度设置为33 kw（所有电器和灯的功率之和）。

• scheme[23]：为了抵抗攻击区分当前密文和未来密文，在每个智能电表的未来密文中增加了一个额外的拉普拉斯噪声Lap(λ)。然而，正如作者所声称的，这会产生很大的误差，随着故障智能电表数量的增加而大大增加。具体来说，如果 w 个智能电表发生故障，w + 1 个拉普拉斯噪声值将额外添加到未来的密文中，这会产生 O( √w + 1) 错误。

• DPAFT：本文克服了这个缺点。从结果图上来看，令n和p分别表示家庭总数和故障智能电表的不同比例。从图中可以看出，在差分隐私的效用方面，p 的数量越大，与[23] 的方案相比，DPAFT的方案越准确。

8.4 容错度的鲁棒性#

• scheme[23]：主要是在GW处存储未来密文，以表现容错度。因此，当故障持续时间 Tper 为 Tb - Ta。如果Tper > B·T，则[23]的系统在Ta+B·T时间点之后不能再容忍故障，因为预先存储的未来密文已经用完，直到故障智能电表Ui再次被恢复。当故障数量激增时，问题会更严重，将不得不采用更大的缓存来提高容错度。

• DPAFT：根据上文的分析，DPAFT方案并没有采用到任何的缓存存储或者未来密文的方式，而是通过计算和加密解密来实现的，因而不会产生上述的问题，能够支持任何长故障周期的数据集成。

8.5 用户添加和删除的效率#

        主要对一系列的方案进行了比较和判别。

        在用户添加和删除方面，作者的方案比 [23] 的方案更有效。在本方案中，为支持用户添加，TA只需为新增用户和CC重新分配密钥材料，为支持用户移除，TA只需为CC更新密钥材料。系统中的其他参与者不需要任何其他操作。

        具体而言，TA只需重新计算变化用户对应的s 0 和s i ，使得$s'0·(\sum{U_i\in U_{unchanged}}s_i+\sum_{U'i\in U{unchanged}}s'i)=1\space mod \space p$ , 然后重新将对应的密钥材料s i 分配给每个变化的用户，并将与每个变化的用户相关的Y i 和s 0 重新分配给CC。

        此外，在作者提出的方案中，更改的用户几乎不需要时间即可生效。

九、相关工作和总结#

        本文提出了一种新的安全数据聚合方案，称为 DPAFT，用于智能电网系统。

        DPAFT在更具挑战性的威胁模型下是安全的，包括外部攻击、诚实但好奇模型下的内部攻击、差异攻击和恶意软件攻击。此外，同时考虑了差分隐私和容错，进一步提高了可靠性和实用性。

        与现有的类似工作不同，作者提出的容错方法是基于一种新颖的巧妙约束关系$s_0\sum_{i=1}^ns_i=1$。有了这种新颖的约束，容错是鲁棒的、高效的和灵活的，高效实现用户更新全动态的真正意义。

        通过广泛的性能评估，作者还证明了 DPAFT 在存储成本、计算复杂性、差分隐私的实用性、容错的鲁棒性以及用户添加和删除的效率方面优于最先进的方案.在未来的工作中，作者准备将数据完整性属性集成到智能电网通信中的隐私保护数据聚合中。

十、笔者评价#

10.1 整理#

        本文主要还是加密方法的介绍，笔者采用如下的图概况，应该会更加直观。

        首先是初始化部分，TA给CC、GW以及U_i进行分配：

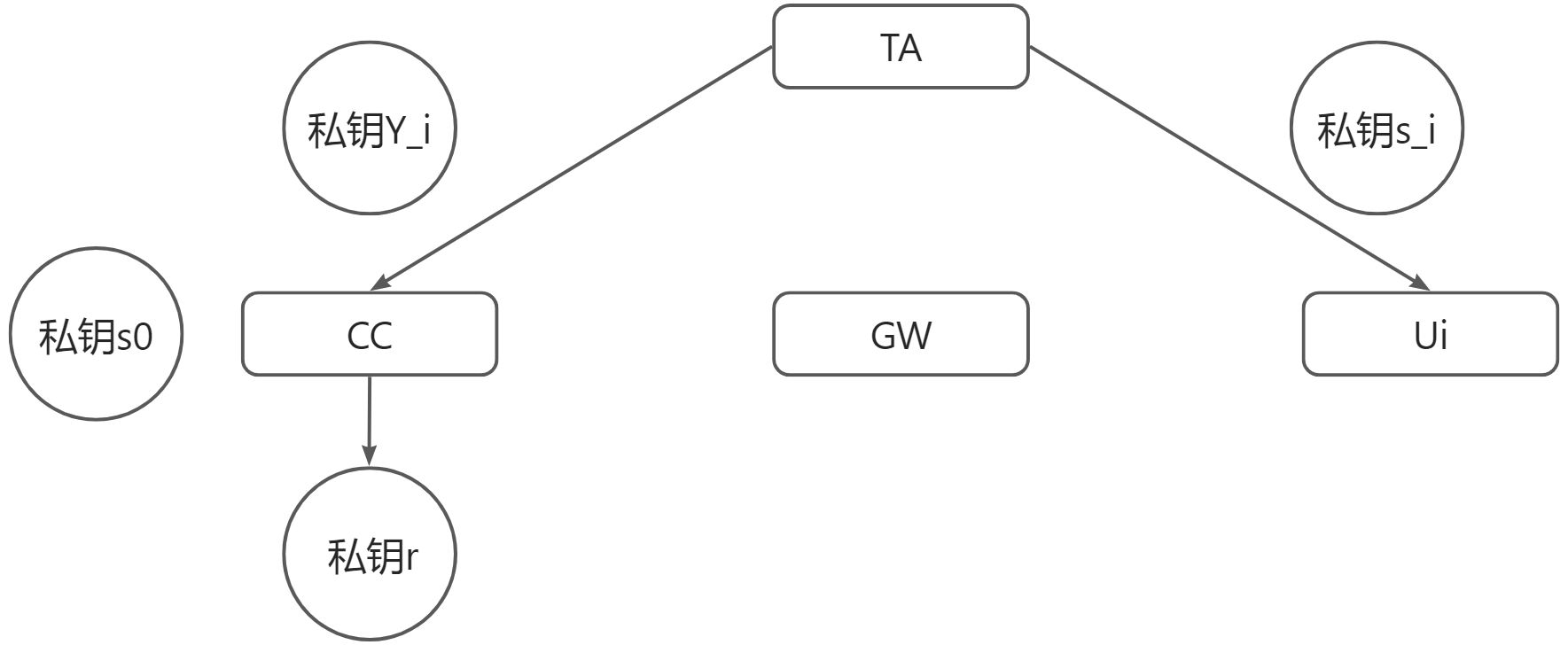
        然后是两种情况下，数据的传输情况。使用了拉普拉斯机制的情形下，流程保持不变。

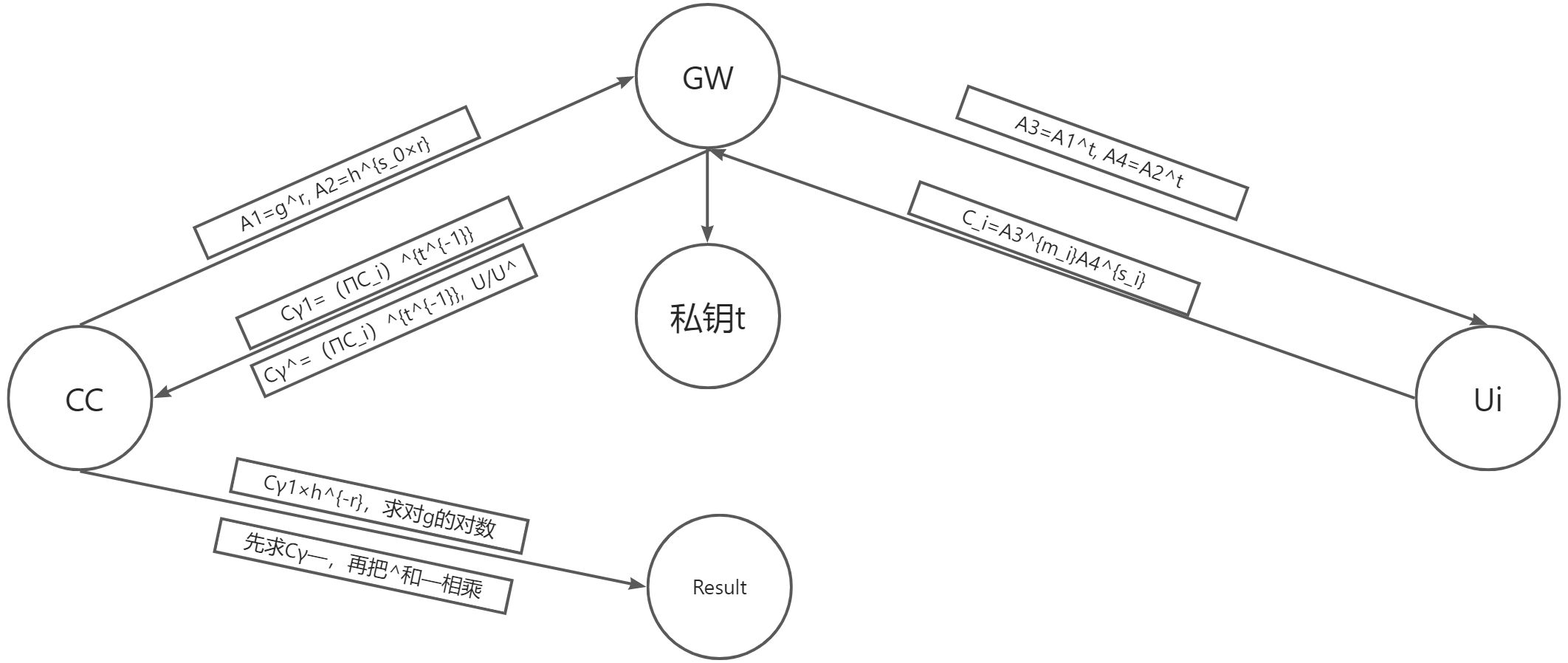
        整体的复杂度应该在于求幂和积分。通过设置多个私钥，使得攻击者即使掌握了某一方的数据，只要私钥没有公开，攻击者拿到的数据里至少会包含两个私钥，使得“暴力破解”的方式不具备可行性。

10.2 创新#

• 差分隐私部分利用了拉普拉斯无限可分机制，这样使得每个用户单独添加噪声再集成后，不至于整体的隐私成本过大，损害数据可用性

• 利用加密密文的方式实现了容错度，不依赖于额外的缓存消耗，对空间的要求更低

• 由TA分配了初始化私钥，在从用户端上传的流中，中间数据始终保持了两个私钥，攻击者即使掌握了某一方的数据，也无法通过暴力破解隐私数据

• 网关只负责转发和基本的运算工作，核心压力较小。这样设计的成本会更低

• 在添加删除用户时，只需要重新分配私钥即可，操作简单

10.3 不足#

• 涉及了较多的幂运算、积分运算，在用户数量较多的时候，时间复杂度可能会高一些，属于时间换空间

• 文中使用的Boneh-Goh-Nissim加密方式是一个有限次全同态加密手段，仅支持1次乘法同态计算。放到现在来看，有了更多的全同态加密手段，应该可以使得保密等级更强。