一、前言#

        差分隐私里一个颇具挑战的问题是：如何生成一个能够在隐私数据里高效捕获有用信息的合成数据集？这个数据集能够在对现有算法不进行任何隐私关照和改动的前提下，允许完成所有的任务。

        作者提出了 PrivSyn 模型，这是首个能够处理常规表格式数据集（包含了100个属，域值大于$2^{500}$）的自动合成数据生成方法。PrivSyn 由一种能够自动地、私密地识别数据相关性的新方法，和一种能够从密集图像模型中生成样本数据的新方法组成。作者还额外地在大数据集上评估了不同的方法来展示他们方法的性能。

二、介绍#

2.1 问题描述#

        DP以前的工作大多集中于为特定的数据分析任务量身定做算法，这种模式不仅耗时，而且需要大量的专业知识，容易出错。

        例如，许多算法被应用于挖掘频繁项集。其中一些错误地使用了稀疏向量技术 (SVT) 导致一些并非符合隐私标准的算法被错误地证明满足 DP标准。要在 DP 的标准下回答 SQL 查询，需要对 SQL 引擎进行修正。再例如，为了训练一个差分隐私的深度神经网络，需要修改SGD算法的步骤。此外，这种范式无法扩展：任务的增加会导致更差的隐私保障，因为每个任务都会揭示更多关于私人数据的信息。

        一个可行的方案是生成一个类似这个隐私数据集，且符合差分隐私标准的合成数据集。因为在公布的数据集上进行的额外数据分析任务是后处理的，所以它们可以在没有额外隐私成本的情况下完成。此外，现有的数据分析算法也不需要更改。

2.2 现有方案#

        对隐私数据，生成合成数据集的方法，现在有以下几种：①使用贝叶斯网络的PrivBayes法；②使用马尔可夫随机场的PGM法。它们都使用了概率图模型。但这两种方法都有局限性。

• 作为一个旨在提供关于联合概率分布的一种紧凑表示的图模型，它在设计上是稀疏的。这种矛盾使得一旦一个结构被固定下来，它就可能会强加一些数据集中根本不存在的条件独立假设。（设计稀疏，随意性大，导致结构固定时数据间产生了某些不该有的关系）

• 由于每个模型都是稀疏的，模型的结构依赖于数据，找到正确的结构对效用至关重要。而贝叶斯网络通常是通过迭代选择交互信息的度量来构建的，而交互信息是高度敏感的，在DP下不可能被精准估计。PrivBayes 为交互信息介绍了一种低敏感度的代理，但计算起来很慢。

• PGM中，没有能提供自动确定图结构的方法，在NIST的挑战中，PGM是使用人工构建的图网络的。

2.3 本文贡献#

        作者为差分隐私合成数据生成提供了一种新的方法：PrivSyn。它主要包括了以下贡献：

        作者没有使用图模型作为一个数据集的概况或象征，而是使用一组数量众多的低度边际来代表一个数据集。例如给定100个属性，作者使用了所有的单向边际和大约500个双向边际（由两个属性确定）。双向边际是一个频率分布表，表示两个属性值的每种可能组合的记录个数。图模型可以被视作一个数据总结的参数化方法，而这种方法是无参的。它的优势在于对属性之间的条件独立做了微弱的假设，只是试图捕捉数据集中的相关关系。

        在DP标准下，这种方法很有吸引力，原因如下：

• 统计记录数字的敏感度很低只有1，统计查询能够较为精确地给出。

• 一个边际揭示了许多个对于“一个统计查询”有着相同隐私成本的统计查询，这很有可能是从一个数据集里在DP标准下发掘信息的最有效的方式。

• 不管使用先进的组合理论还是零—集中DP，在隐私预算相同的前提下，添加到每个边际里的噪声的方差只和边际的数量成线性关系。

• 当一个属性被包含在多个边际中时，人们可以使用平均法来减少误差。因此，人们可以在合理的精度下获得大量的边际。

        挑战在于：

• 如何选择哪个边际来使用？

• 如何在给定噪声边际的前提下合成数据集？

        作者提出了一种自动且私有地选择边际的方法。作者首先提出了指标 InDif，用于衡量成对属性之间的关联。InDif易于计算，拥有较低的全局敏感度，基于这一点，作者提出了一种贪心算法来选择构成边际的属性对。

        作者提出了一种能够迭代更新一个合成数据集的方法，来使得其能够匹配由边际定下的目标。当属性的数量足够少，以至于可以直接存储和操作完整的或然率表时，可以使用乘法更新等方法来实现。但如果属性数量很大时，要表示完整的或然率表是不可行的。

        作者方法的关键点在于，把一个正在合成的数据集想象成一个正在被估计的联合分布的代理，然后直接操控这个数据集。

        给定一个噪声边际的集合，当每个属性在集合中都匹配到了单向边际信息时，开始生成一个随机的生成数据集，然后逐渐“按摩”合成数据集，使得它的分布越来越靠近每一对边际。作者把这个问题建模为一个网络流的问题，并提出了GUM方法，一种“按摩”数据集的方法，使其与所有的噪声边际相一致。

• 一个简单但是有效的方法来捕获数据集之间的关系。

• 一个新的方法来自动且私有地选择捕获足够关联的边际。

• 一个数据合成算法GUM，也能够独立使用来处理密集图像模型。

• 一个扩展评估，它能够证明提出的方法在现实数据集上的性能提升，然后帮助我们直观地理解不同的技术。

三、前置知识#

3.1 差分隐私#

        具体内容不再赘述，这里使用的是(ε，δ)-DP定义。

3.2 高斯机制#

        简单来说，可以用如下公式表示：

3.3 通过 0-集中差分隐私 的组合#

        中心思想是把 (ε，δ)-DP 和 renyi分歧 连接起来，这样就能够有效使用 renyi分歧的性质来获得更紧的组合特性。

【定义】：一个随机机制是A 是 p-zero集中差分隐私 ，当且仅当对于任意两个邻近数据集 D和D’, 以及所有的 α∈(1, ∞)，有：

        其中，$D_α(A(D)||A(D'))$是分布A(D)和A(D’)的 α-renyi 分歧。 $L^{(o)}$ 是概率密度函数 $f(x)=log\frac{Pr[A(D)=X]}{Pr(A(D')=x)}$ 的隐私损失随机值。

        zCDP具备一些简单的线性组合性质，同时还可以与高斯机制组合：

【定理1】：如果随机机制A1和A2分别满足 p1-zCDP 和 p2-zCDP，那么它们的线性组合 A=(A1, A2)满足 (p1+p2)-zCDP

【定理2】：如果A提供了 p-zCDP，那么对于任意的δ>0，A满足$(p+2\sqrt{plog(1/\delta)},\delta)-DP$

【定理3】：一个提供了噪声 $N(0,\Delta_f^2\sigma^2)$ 的高斯机制满足$\frac{1}{2\sigma^2}-zCDP$

        根据这三条定理，给定 ε 和 δ，我们就能够为每个任务计算噪声的总量。

• 首先使用定理2，计算满足条件的总共p值。

• 然后使用定理1，来为每个任务 i 分配一个pi。

• 最后，使用定理3来为每个任务分别计算 σ。

3.4 任务定义#

        在本文中，考虑以下问题：给定一个数据集Do，我们想生成一个与Do在统计学上相似的合成数据集Ds。生成合成数据集Ds允许数据分析师在同一组发布的数据上处理任意种类的数据分析任务，这比之前专注于优化特定任务的输出的工作更为普遍。

        更正式地说，一个数据集D是由n条记录组成的，每条记录有d个属性。如果f(Ds)与任何函数f(Do)接近，则称合成数据集Ds与Do相似。在本文中，我们考虑三种统计措施：边际查询、范围查询和分类模型。特别是，边际查询抓住了属性子集的联合分布。一个范围查询计算其对应值在给定范围内的记录数量。最后，我们还可以使用合成数据集来训练分类模型并测量分类的准确性。

四、一种隐私数据合成的框架#

        为了在差分隐私框架下生成合成数据集，首先需要把任务转变为：评估低敏感度 Δf 下的损失函数 f 。

        一种直观的方法是，获取噪声的全分布，也即，所有属性的联合分布（全分布）。如果给定分布的具体信息，那么只需要从分布中采样，就能够生成一个合成数据集了。但当属性的个数太多时，计算乃至存储的开销都会大得惊人。这种方法并不合适。

        为了解决这个问题，一种可行的方法是评估许多低度的联合分布（也叫边际，通常只包含属性的一个子集的分布）。为了生成一个合成数据集，一共需要以下四个步骤：边际选择、添加噪声、后期处理、数据合成。如下图所示：

4.1 数据合成#

        为了合成一个数据集，现有的工作主要使用“图模型”来模拟数据的生成。

        比如，PrivBayes 使用了一个不同的隐私贝叶斯网络。它可以用有向图来表示。在图中，每个节点v代表一个属性，从u到v的每条边都对应于Pr[v|u]，即u导致v的概率。由于每个属性可以取多个值，因此需要所有可能的Pr[v=y|u=x]。当一个节点v有一个以上的节点U={u1,…,uk}与之相连时，需要Pr[v|U]来对v进行采样。为了对一条记录进行抽样，我们从内度为0的节点开始，然后按照贝叶斯网络指定的生成顺序遍历图形以获得其余属性。

        最近，[41]提出从“差分隐私-马尔可夫随机场（MRF）”中采样。与贝叶斯网络不同的是，MRF由无向图表示，每条边（u，v）包含联合分布Pr[v,u]。 此外，在这个模型中允许循环甚至成环。 更复杂的结构能够捕捉到更高维度的相关性，但也会使采样更具挑战性。PGM的主要缺点是当图很密集时，交界树中的cliques域可能太大，无法处理。

4.2 边际选择#

        为了生成一个图像模型，形如Pr[v,u]的联合分布是必须的。目标是捕获所有的联合分布，但是由于DP的复杂性，更多的边际将导致更多的噪声。这并不是我们所希望的。

        PrivBayes 通过构建贝叶斯网络来选择边际。首先随机分配一个属性作为第一个节点，然后用指数机制逐一选择其它属性。原始贝叶斯网络使用交互信息作为衡量标准来选择最相关的边际。在DP的环境里，交互信息的敏感度很高，为了降低其敏感性，[53]的作者提出了一个接近于交互信息的函数来代替。

        PriView 使用了一种数据独立方法来选择边际。选择一组“使得所有的属性对或者属性三对都被包含在一些边际中”的最小边际。当一些属性是独立的时候，捕捉它们之间的关系实际上增加了噪声量。这种方法的适用性并不大。

4.3 添加噪声和后处理#

• 添加噪声：给定边际，下一步就是往里面添加符合DP的噪声。经典的方法是将隐私预算平分到这些边际中，然后添加拉普拉斯噪声。

• 后期处理：DP噪声的引入带来了不一致性：①一些估计的概率值有可能为负；②估计的概率之和并不为1；③两个包含共同属性的边际存在不一致性。PrivBayes中，负概率被转换为0。在PGM中，一致性是由马尔可夫随机场的估算程序隐含地处理的。

五、差分隐私边际选择#

        在获取边际的阶段，有两个主要的错误源：①当错过一些边际时，存在信息损失；②由DP引起的噪声错误。它们分别对应了“PrivBayes的信息遗漏”、“PriView的噪声过多”两个问题。

        作者提出了一个即使在很低的隐私预算下也能获取更多有效关联性的选择边际的算法：DenseMarg。

5.1 依赖性测量#

        我们首先需要一个度量来评估关联性等级。贝叶斯网络使用交互信息作为度量，但敏感度太高了。[53]提出的方法，计算太慢了。

        作者提出了**“独立性差异”(Independent Difference, also InDif)**。对于任何两个属性a,b，InDif计算 实际的2维边际Ma,b 和 假设独立的2维边际Ma×Mb 之间的距离 l1，即：

        如下图所示：

        InDif的值为 0.8*n，其中n为记录的数量。使用 InDif 的优点是它很容易计算，而且具备很低的敏感度。

• 定理4：InDif 度量的敏感度为4：Δ_{InDif}=4

• 定理5：给定 d 个属性，发布所有在高斯噪声N(0,8m/p’)下的 m=d(d-1)/2 InDif 分数，都符合p’-zCDP。

5.2 边际选择#

        在给定 InDif 之后，下一步就是选择具备高相关性的属性对，然后使用高斯机制对这些对发布边际。这里一共有两个错误源：①高斯噪声引入导致的噪声错误；②当某些边际没有被选择时产生的依赖性错误。这两者是不互存的关系，如果选择全部的边际，那么错误①会极速增大，而错误②不会发生；如果选择很少的边际，则错误会由②主导。

• 问题规格化：给定 m 个属性对，每一对 i 分配了一个值 x_i，如果为1，表示被选中，0表示没被选中。定义 ψi 为引进高斯机制导致的噪声错误，Φi 为依赖性错误。这样问题就可以写成如下所示的形式：

        注意到越大的 InDif 产生越大的依赖性错误，因此，可以把Φi 近似为 InDif+N(0,m^2p’^2)，这将在优化问题中被固定。

        噪声错误ψ_i取决于分配给一对i的隐私预算p_i。给定真实边际Mi，添加规模为1/pi的高斯噪声，来获得pi-zCDP。

• 定理6：(1)边际M具有敏感性ΔM=1；(2)发布边际M的噪声N(0,1/2ρI)满足ρ-zCDP。

        为了使得 ψi 和 Φi 具备可比性，我们使用高斯噪声在边际i上的期望 l1 误差。如果边际的大小为ci，在添加了规模为σi的高斯噪声之后，我们期望能够看到l1错误:$c_i\sqrt{\frac{2}{\pi}}\sigma_i$. 这样，在隐私预算ρi，$\psi_i=c_i\sqrt{\frac{1}{\pi ρ_i}}$ 下，问题就转化为了：

• 动态隐私预算分配：我们首先假设所有的配对都是被选择的，这样问题可以转化为：

        我们可以引入拉格朗日函数：$L=\sum_i\frac{c_i}{\sqrt{ρ_i}}+\mu·(\sum_iρ_i-ρ)$ ，对每个ρi求偏导，有：$ρ_i=(\frac{2\mu}{c_i})^{-2/3}$，其中通过解方程，得到：$\mu=(\frac{ρ}{\sum_ic_i^{2/3}})^{-3/2}$，这样：$ρ_i=\frac{c_i^{2/3}}{\sum_jc_j^{2/3}}ρ$ 。

        也即，为了获得最小的噪声错误，分配的隐私预算应该和神经元数量（或者叫边际的规模）的2/3次方呈正比。

• 贪心算法：如下图所示：

【已有】：所有属性配对的 InDif 分数<Φi>，所有的边际规模，所有的隐私预算 ρ

【输出】：为每个i∈{1,…,m}决定一个xi，使得整体的错误最小化。

【过程】：

①首先定义符号：X：输出集合；t：迭代次数；$\overline{X}$：{1,…,m}\X

②从 $\overline{X}$ 里选出一个数i，然后把ρ分配给i和X里的边际；

③计算Et，并选出使得Et最小的那个i；

④如果这次迭代结果比上次小，那么把它加入到X里面，进行下一次迭代。否则停止迭代。

算法必定会停止，因为随着边际的不断加入，噪声错误会激增。

• 组合边界：至此考虑的都是2-向的情况，如果某些边际只包含了一些很小的可能结果（例如二分的属性），那么扩充成多维边际就能够捕获更多的信息。

        给定X这个从算法1中选取的边际的索引，我们首先把每个索引转化成其对应的一对属性，然后构建起一个图G，每个节点代表 一个属性，一条边代表了一个配对。然后找到所有规模大于2的cliques，如果它的规模小于阈值γ，并且和现有的已经选择好的属性并没有太多的重叠（大于2个），那么我们就把clique中包含的2向边际合并成一个多向边际。

        我们首先确定图G中所有可能的cliques，并按其属性大小降序排序。然后，我们检查每个clique c，以确定是否将其合并。如果该clique具有较小的域大小（小于阈值γ），并且不包含超过2个已经在选定的属性集S中的属性，我们就包括这个clique并删除其中的所有2向边缘。

5.3 后期处理#

        主要目的是为了保持噪声边际的一致性。

• 不均匀隐私成本分配下的一致性：当不同的边际有一些共同的属性时，这些属性可能会被多次估计，那么这种情况下将其视为一个整体再取均值，可能比单独采用每个它们，结果会更精确。作者采用了加权均值来计算，为每个边际 i 分配一个权重 wi。加权均值的方差可以如下表示：$\sum_iw_i^2·\frac{g_i}{ρ_i}$，其中，ρi是隐私预算成本，gi是对A上边际的一个单元的贡献的单元数。高斯机制的方差为1/ρi。这样问题可以转化为：

        和上面类似，引入拉格朗日式子，我们可以得到最合适的结果：$w_i=\frac{ρ_i/g_i}{\sum_iρ_i/g_i}$

• 整体的一致性：除了边际分布直接的不一致，整体上可能还包含了一些无效的分布（比如一些概率估计为负数，且总和不等于1）。一个可能的方法是，一最小的l2距离将其投影到一个有效的分布，可以实现最大似然估计。

        同时处理以上两种不一致带来了困难：一种不一致性刚处理完，另一种不一致性一处理，前一种的一致性就被打破了。作者进行了多次迭代来确保结果。

六、合成数据生成#

        给定一个噪声边际的集合，这一步的目标是生成一个新的数据集Ds，使得Ds的分布和噪声边际的分布保持一致。之前的方法大多是采用图模型，使用采样算法来生成合成数据集。这种方法的问题是，如果这是一个密集图的话，复杂度会很高，算法失效。为了解决这个问题，作者选择初始化一个随机的数据集，然后不断更新记录来使得它和噪声边际保持一致。

6.1 Strawman 方法：最小成本流（MCF）#

        一个由一系列属性标识的边际，是每个属性值的可能组合的频率分布表。更新过程可以理解为一个图形流问题。

具体来说，给定一个边际，我们就能够构造出一个双边图。左侧表示当前Ds的分布，右侧表示由边际指定的目标分布。每个节点对应于边际中的一个单元，并且与一个数字相关联，如下所示：

        MCF方法执行图的最小成本流，并且通过改变流的记录值来更新Ds。

        作者通过迭代所有的噪声边际，并且重复多次过程，直到更改量很小为止。一个很直观的使用MCF的看法是，更新操作对Ds进行了最小的改动，俄日且保持了Ds和源的一致性。MCF方法可以通过现成的线性规划求解器解决。当所有边际都被检查时，将随机洗牌整个数据集Ds。

6.2 逐渐更新方法GUM#

        作者发现MCF方法的收敛性并不好。出现这样的原因，作者认为，MCF在每一步里都经常改变Ds以此来与当前的边际保持完全一致。这一步会把目标边际的错误趋向于0，但会放大其他边际的错误。

        作者提出了GUM方法。GUM和MCF存在着诸多不同。

        首先，GUM 不会要求Ds在每一步里都和给定的边缘完全一致。相反，它以乘法的方式来改变Ds，这样如果一个神经元的初始频率很大，那么对它的改变会更多。具体来说，设置一个参数α，对于所有值低于预期的神经元（根据目标边缘），增加最多目标记录的α倍，也就是min{n^t-n^s，αn^s}。n^t是边际的数量，n^s是Ds的数量。相同的，对于高于预期值的神经元，减少最多β倍，也就是min{n^s-n^t,βn^s}。

        其次，需要使用“替换”和“复制”的组合方法来更新Ds。尤其是当合成数据集逐渐靠近源分布时，方案会更青睐“复制”，因为“替换”会破坏联合分布，而实验证明“复制”能够有效提高收敛性能。

6.3 提高收敛性能#

• 逐渐减小α：随着迭代次数的增加，更新速率α应该逐渐变小，以此来使得结果收敛。有诸多的方法来设置α：

• step decay：$\alpha=\alpha_0k^{[t/s]}$, a0 是初始值，t是迭代次数，k是衰减速率，s是每一步的规模。每s次迭代，减小α为原来的k倍。

• Exponential decay：$\alpha=\alpha_0e^{-kt}$，k是一个超参数。每一步迭代，都减小一次α。

• Linear decay：$\alpha=\frac{\alpha_0}{1+kt}$

• Square root decay：$\alpha=\frac{\alpha_0}{\sqrt{1+kt}}$

        经过实验，step decay 的结果最好。

• 属性合并：在算法2里输出的边际中，有些节点只有一个值，这表示相关的属性只被包含在一个边际中。对于这些属性，没有必要加入更新过程，而是可以在生成数据集之后再添加进去。

• 分与和：当隐私预算较低时，所选边际的数量相对较少，并且依赖图是以几个不相交的子图的形式存在的。在这种情况下，可以对每个子图应用GUM，然后连接相应的属性。Separate and Join技术的好处是，一个子图中的边际的收敛性能不会受到其他子图中边际的影响，这将提高整体的收敛性能。

• 过滤与合并低计数的值：一个属性可能由很多的可能值，但他们中的大部分都是low-counts的或者在数据集中没有出现。直接使用这些属性来获得成对的边缘值可能会引入太多的噪音。作者的想法是，花一部分隐私预算来获得嘈杂的单向边缘值。之后，我们保留计数高于阈值θ的值。 对于低于θ的值，我们把它们加起来，如果总数低于θ，我们给所有这些值分配0。如果它们的总数高于θ，那么我们就创建一个新的值来代表所有具有低计数的值。在合成数据集之后，这个新的数值被它所代表的数值取代，使用的是噪声单向边际。阈值被设定为θ=3σ，其中σ是添加到单向边际中的高斯噪声的标准偏差。

6.4 整合：PrivSyn#

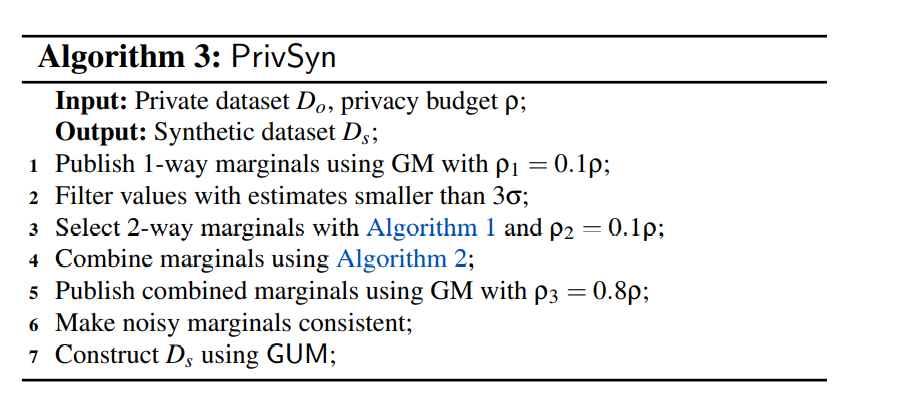
        整个过程可以分为三个部分：

• 第一部分是打印出所有的单向边际，使用过滤与合并方法，来把低计数的值组合或者舍去

• 第二部分是在差分隐私标准下选择边际。边际选择方法 DenseMarg 由两个算法（2向边际选择和边际组合）组成。

• 第三部分是获得噪声组合边际，使用它们在不消耗隐私预算的前提（这里是后期处理）下，生成合成数据集Ds。

七、评估#

7.1 实验设置#

• 数据集：在以下四个数据集中进行了实验：

• UCI Adult、US Accident、Loan、Colorado

• 具体配置：

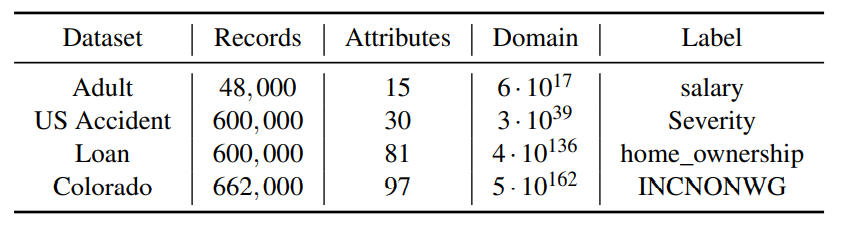
• 任务和度量：在以下三个数据分析任务中评估了合成数据集的性能表现：

• 边际选择：计算了所有的二向边际，使用平均 l1 误差来评估性能

• 范围查询：随机抽样1000组范围查询，每个包含3个属性。使用平均 l1误差来衡量性能。特别地，计算如下式子：$\frac{1}{Q}\sum_{q_i\in Q}|c_i-\hat{c_i}|$，其中Q是随机抽样查询的集合，$c_i\;\&\;\hat{c_i}$ 分别是原始数据集和合成数据集中落在查询qi范围内的记录的比率。

• 分类：使用合成数据集来训练SVM分类模型，并使用错误分类率来衡量性能。

• 比较者：从 PrivSyn 的各个部分来与其他方法进行比较：

• 边际选择方法：DenseMarg Vs PrivByes

• 噪声添加方法：Weighted Gaussian Vs Equal Laplace Vs Equal Gaussian

• 数据合成方法：PrivSyn Vs PrivBayes Vs PGM

• 参数设置：step size = 2.0, sample size = 1000, δ = 1/n^2 where n = the number of records in original dataset.

7.2 端到端比较#

        对于成对边际任务，PGM和PrivBayes的性能非常接近PrivSyn，这意味着这两种方法可以有效地捕获低维相关性。但是，范围查询任务和分类任务的性能比PrivSyn差得多，因为范围查询和分类任务需要更高的维相关性。PrivSyn可以有效地保留低维和高维相关性。

        DualQuery的性能明显比其他方法差。原因是生成每个记录会包含一部分隐私预算，这限制了DualQuery生成的记录数量。在实验中，在所有设置中，DualQuery生成的记录数量小于300。当隐私预算较低时，例如 ε = 0.2，生成的记录的数量小于50。记录数量不足将导致所有三个数据分析任务的性能不佳。

7.3 边际选择方法的比较#

        对于所有数据集和所有数据分析任务，作者提出的 DenseMarg 方法始终优于 PrivBayes(InDif)。在范围查询任务中，DenseMarg将 l1 误差减少了约50%，这比 成对边际发布任务 里要重要得多。这是因为 DenseMarg 的范围查询包含3个属性，这需要比成对边际 (包含2个属性) 更高的维相关性信息。

        DenseMarg 通过选择比 PrivBayes(InDif) 更多的边际来保留更高的维度相关性。在所有设置中，DenseMarg 在隐私设置和非隐私设置中的性能都非常接近。原因是 DenseMarg 倾向于选择具有高InDif的边缘集，并且添加中等水平的噪声不太可能显着改变该边缘集。在作者的实验中，在大多数情况下，隐私设置和非隐私设置之间所选边际的重叠比率大于85%。这表明 DenseMarg对噪声非常可靠。

7.4 噪声添加方法的比较#

        对于所有数据集和所有数据分析任务，作者提出的加权高斯方法要优于其他两种方法。当 ε 较大时，加权高斯的优势会增加。

        在作者的实验中，加权高斯方法和等高斯方法都使用zCDP来计算每个边缘的噪声方差，主要区别在于加权高斯根据神经元的数量来分配隐私预算，而等高斯则将隐私预算平均分配给所有边缘。实验结果验证了我们在第5.2节中的分析，即加权高斯是最佳的隐私预算分配策略。

7.5 合成方法的比较#

        MCF和GUM都利用DenseMarg选择的密集边际，而MCF的性能甚至比使用备用边际的PGM方法和PrivBayes方法还要差。原因是，在每次迭代中，MCF都会强制合成数据集Ds完全匹配边际。这将严重破坏其他边缘所建立的相关性。GUM通过在每次迭代中逐步更新边缘并使用复制技术来保留其他边缘的紧密关系。

八、相关工作#

• Graphal Model Based Methods

• Game Based Methods

• Deep Generative Model Based Methods

• Theoretical Results

九、总结相关#

9.1 本文的流程#

        本文的整体的流程如下：

        首先是过滤和合并，把边际里计数低于阈值的合并起来，如果值仍旧低于阈值，那么直接舍弃；否则合并成一个新的边际来代表这些边际。这一步是起过滤作用，在整个数据集里，单向、低-计数的边际越多，那么不经过任何处理，往里面添加噪声的话，噪声的规模会很大。因此首先需要进行过滤处理。

        其次是在差分隐私标准下选择边际。作者在这里抛弃了高维的边际，而是采用了2维边际。作者提出了度量标准：InDif，用来评估 实际2维边际 和 假设2维边际 之间的距离。这样便可以根据 InDif 来选择边际对了。作者在这一部分首先提出了评估的标准，也即：

        ψ表示噪声误差，主要由引入的噪声产生；Φ表示依赖性误差，主要由遗失的依赖、一致性的差别产生。根据定义，Φ可以由InDif的表达式表达，ψ由 l1 误差的定义给定。这样便诞生了算法1。然后和第一步中相似的思路，把一些计数很小的2向边际合并，这样便诞生了算法2。

        然后是进行后处理，这一步主要处理一致性的问题，包括“引入噪声导致概率和不为1或者概率为负”以及“部分属性重叠计算导致的不一致性”。

        在后处理完毕之后，便开始进行最后的数据集生成，这里采用了逐渐更新方法GUM。采用替换和复制的方式，来更新数据集，使得生成数据集与分布保持一致。

9.2 分析#

• 主要贡献：

• 提出了一种“关联性度量”的标准，即 InDif；

• 提出了一种贪心算法，来自动过滤、捕捉、选择、合成符合要求的边际；

• 全文两处进行了权衡：最小化误差（噪声误差和依赖性误差的权衡）；一致性权衡（属性重叠、引入噪声导致的概率和不为1或概率为负）

• 基于以上3点，作者的方法在敏感度下要胜过采用了交互信息的贝叶斯法，在操作上要胜过手动的马尔可夫随机场。同时由于使用的是贪心算法，算法复杂度要远低于以上两者。

• 有针对低计数、单维度的边际的处理（过滤和合并、不一起处理而是在最后再添加单维度的边际）。

• 不足之处：

• InDif 目前还只能处理表格形式的数据，对于图像问题还需要进一步的研究以及映射。

• 为了避免计算复杂度的过高，作者抛弃了一些高维度的边际。这使得算法本身会损失了一些高维度的相关性。