一、(ε, δ)-DP 的回顾# (ε, δ)-DP 是经典的差分隐私范式,其一般格式是,对任意两个邻近数据集 D 和 D’,都有:
P r [ M ( D ) ∈ S m ] ≤ e ϵ × P r [ M ( D ′ ) ∈ S m ] + δ P_{r}[M(D)\in S_{m}]\leq e^{\epsilon}×P_{r}[M(D')\in S_{m}]+\delta P r [ M ( D ) ∈ S m ] ≤ e ϵ × P r [ M ( D ′ ) ∈ S m ] + δ 这个式子是通过 相对熵 推导出来的,具体可以看这里的解析 。
通过这道公式,人们可以设计出诸多不同的”机制“,来对数据集进行隐私保护,例如 拉普拉斯机制 和 高斯机制。前者通过添加具备”长尾“特性的拉普拉斯噪声来保护隐私,对离散型的数据具有比较友好的作用;后者的”对称特性“则更加适合用来保护连续数据的隐私,例如均值、方差…
但是在面对”组合查询“这类的问题的时候,上述的 (ε, δ)-DP 范式就产生了问题:基于散度的定义式,难以给出直观的组合机制应该遵循的规则,只能使用放缩法来给出一个近似的上界。这方面的研究包括了 ”强组合定理“、”Moment Accountant“和”Renyi Accountant“等。
这些组合机制大部分都是针对”期望“的高阶范式进行研究。例如:
”强组合定理“主要利用”隐私损失期望的上界“和”Azuma不等式“给出组合机制;
Moment Accountant 将期望看成”一阶原点矩“,通过高阶的展开式进行推导;
Renyi Accountant 通过考察 ”散度“的定义式,从高阶矩的定义出发,重写了差分隐私的表达式…
具体可以参考这篇的总结文字 。总而言之,这些方法优化的思路就是:在机制中添加噪声,如果数据本身具备高维的特性,那么对应的噪声机制也应该考察维度的特性。在高阶展开式里添加更紧的上界,从而在符合DP的前提下,减少噪声带来的精度损失。问题在于:这些方法大部分都从”高阶“的角度来进行优化,并不直观;偏离了”差分隐私“的形象描述,比较抽象,因而其目的大多是为了找到一个更紧的上界作为组合机制的近似。
二、权衡函数——假设检验的引入# 在”强组合定理 “的文章中,作者引入了”假设检验“。但原文只是将其作为一个测试的直观标准。而本篇的作者则基于”假设检验“进行了更加深入的推导。
首先,假设 S 和 S’ 是一对邻近数据集,M是一个隐私机制,P 和 Q 是机制 M 应用于这一对邻近数据集的概率分布。 那么对于攻击者而言,数据自然存在两种假设:
H 0 : 落在 S 中, H 1 :落在 S ’ 中 H_0:落在\;S \; 中,H_1:落在 \;S’\; 中 H 0 : 落在 S 中, H 1 :落在 S ’ 中 这样一来,攻击者的判别错误就可以分为两个类别:
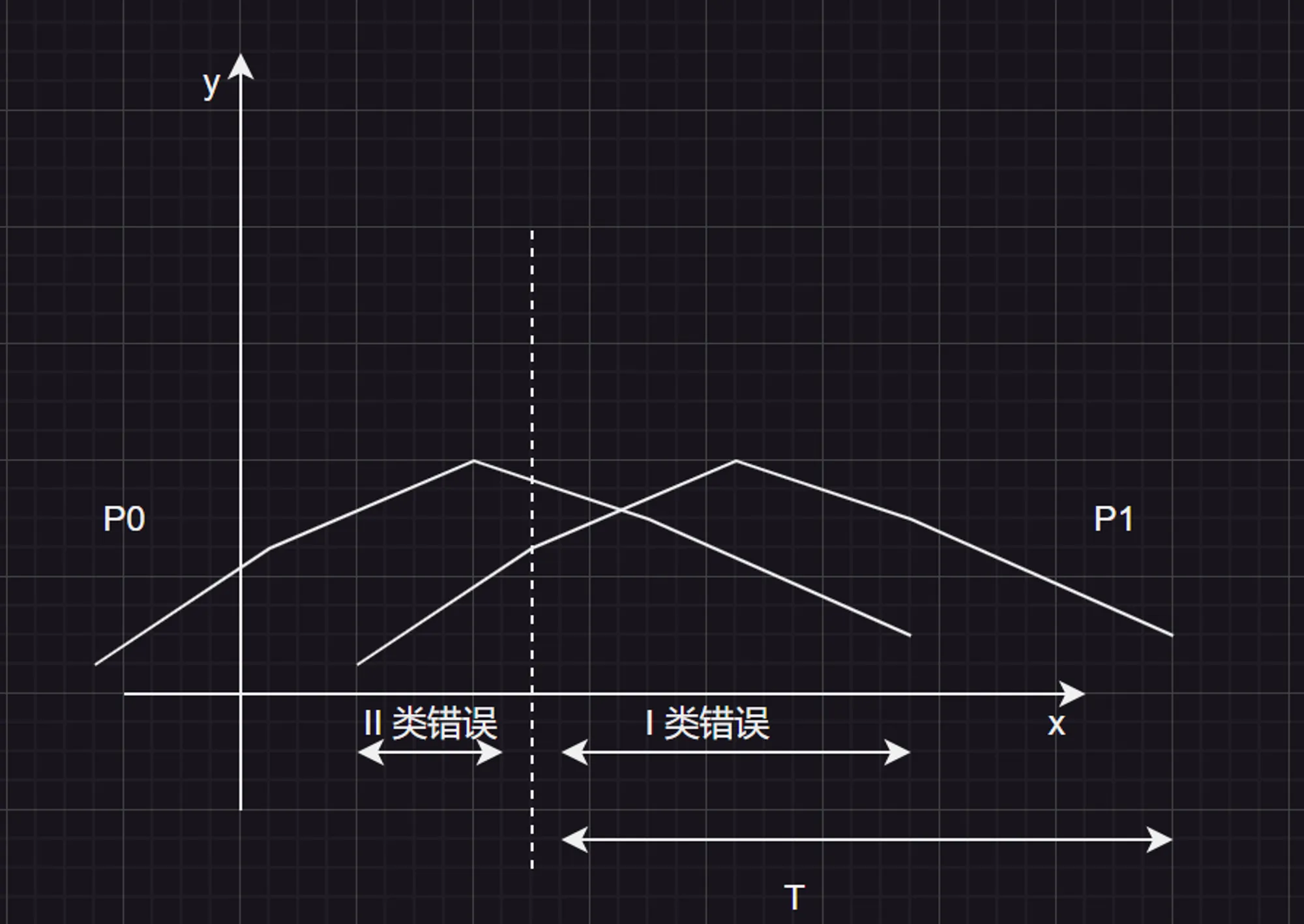
我们将其分别记为 一类错误 和 二类错误。如下图所示,我们可以给出对应的示意图:
在这个图中,我们假设 T 区域的为“拒绝域”,也就是拒绝假设 P0,接受假设 P1。根据这一点,很容易划分出 “I 类错误” 和 “II 类错误”:显然,P0 在 T 内的点,都是 I 类错误的;P1 在 T 左侧的点,都是 II 类错误的。而随着 T 区域的不断右移, I 类错误的概率会不断缩小,II 类错误的概率会逐渐增大。从而在这两类错误间,形成了一个“权衡”关系: trade-off。
在假设检验中,我们通常会给定一个常量来判定”显著性水平“,记为 α。考虑一个”拒绝零假设的规则“ Φ(0 ≤ Φ ≤ 1),那么 I 类假设 和 II 类假设就可以表示为:
α ϕ = E P 0 [ ϕ ] , β ϕ = 1 − E P 1 [ ϕ ] \alpha_{\phi}=E_{P_0}[\phi], \;\; \beta_{\phi}=1-E_{P_1}[\phi] α ϕ = E P 0 [ ϕ ] , β ϕ = 1 − E P 1 [ ϕ ] 而 I 类错误 和 II 类错误的一个限制条件是:
α ϕ + β ϕ ≥ 1 − T V ( P 0 , P 1 ) \alpha_\phi+\beta_\phi \geq 1-TV(P_0,P_1) α ϕ + β ϕ ≥ 1 − T V ( P 0 , P 1 ) 其中,T V ( P 0 , P 1 ) TV(P_0, P_1) T V ( P 0 , P 1 ) ∣ P 0 ( A ) − P 1 ( A ) ∣ | P_0(A) - P_1(A) | ∣ P 0 ( A ) − P 1 ( A ) ∣
现在,我们需要一个标准来量化假设检验的难度,这样我们就可以利用这个值来作为隐私保护的标准。作者给出的表达式为:
T ( P , Q ) ( α ) = i n f { β ϕ : α ϕ ≤ α } T(P,Q)(\alpha)=inf\{\beta_\phi :\alpha_\phi\leq \alpha \} T ( P , Q ) ( α ) = in f { β ϕ : α ϕ ≤ α } 这个表达式的意思是,在框定 α 的前提下,考虑可实现的最小 II 类误差。我们将符合这样要求的函数记为 ”权衡函数(trade-off function)“。显然,如果这个函数值越大,就表明在给定显著性水平的前提下,最小的 II 类错误也越大,就越难区分两个分布了。
对于函数 f : [ 0 , 1 ] → [ 0 , 1 ] f :[0,1]→[0,1] f : [ 0 , 1 ] → [ 0 , 1 ]
f 是凸函数 ( convex function )
f 是连续的
f 是非递增
f ( x ) ≤ 1 − x f o r x ∈ [ 0 , 1 ] f(x) \leq 1-x \;\;for\;\; x \in [0,1] f ( x ) ≤ 1 − x f or x ∈ [ 0 , 1 ]
三、f-DP 的定义# 在 [0,1] 上,如果均有 g ( x ) ≥ f ( x ) g(x) \geq f(x) g ( x ) ≥ f ( x ) g ≥ f g \geq f g ≥ f
这样我们就可以给出 f-dp 的定义了:
l e t f b e a t r a d e − o f f f u n c t i o n , M i s s a i d t o b e f − d p i f : T ( M ( S ) , M ( S ′ ) ) ≥ f , f o r a l l n e i g h b o r i n g d a t a s e t s S a n d S ′ let \; f \; be \; a \; trade-off \; function,\;M \; is \;said\;to\;be\;f-dp\;\;if:\;\\ T(M(S),M(S'))\geq f,\;\\for\;all\;neighboring\;datasets\;S\;and\;S' l e t f b e a t r a d e − o ff f u n c t i o n , M i s s ai d t o b e f − d p i f : T ( M ( S ) , M ( S ′ )) ≥ f , f or a ll n e i g hb or in g d a t a se t s S an d S ′ 这个 f-dp 的定义是在说明:对于机制 M,如果基于发布的信息,区分任意两个临近数据集的难度,至少不弱于基于单个平局区分 P 和 Q 的难度,那么这个机制就是 f-dp 的。显然,f-dp 具有对称性。
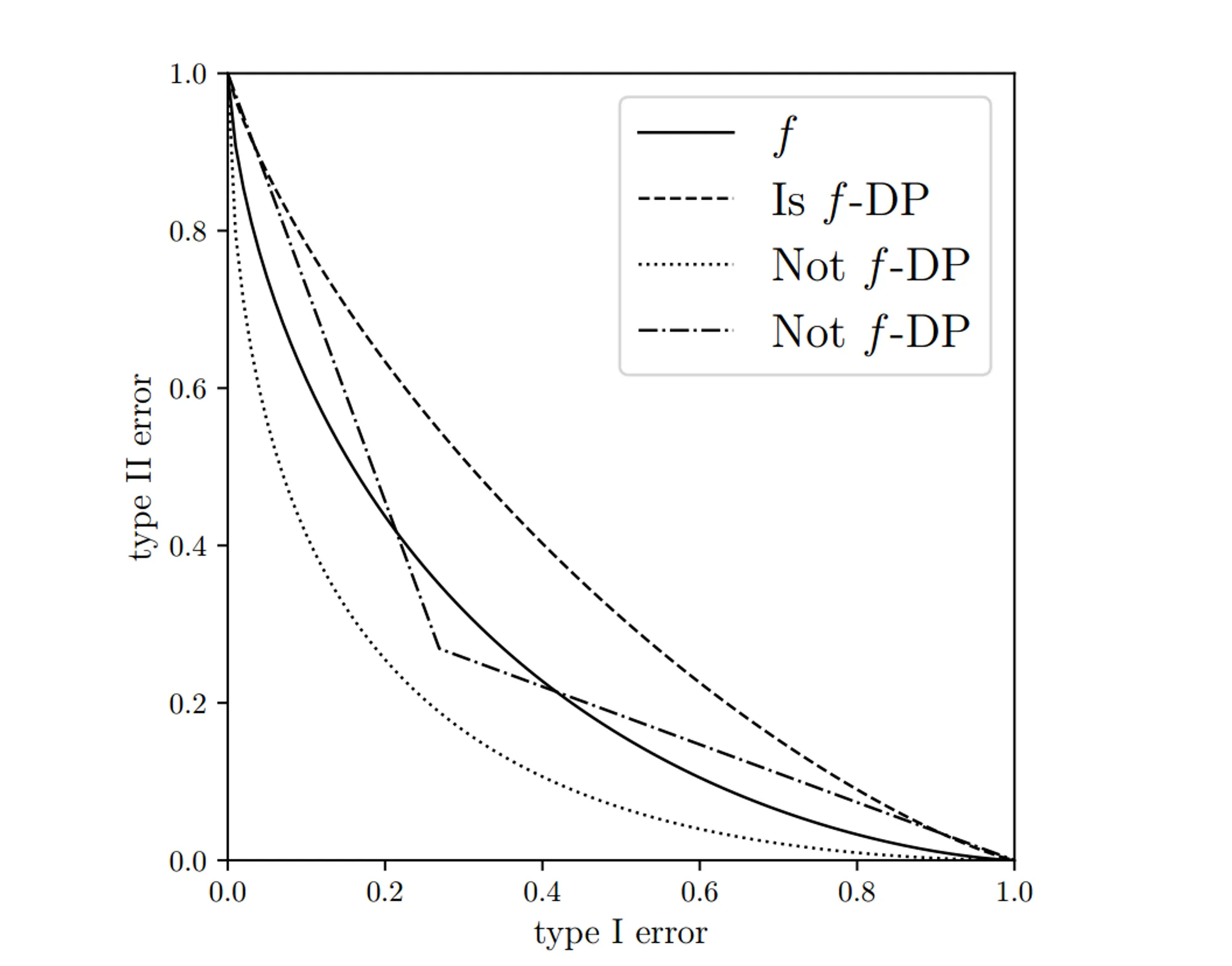
参考作者给出的这张图:
这张图里给出了四份曲线。其中,实线是作为标准的权衡函数 f,只有全部在 f 上面的虚线才是符合 f-dp 的,部分位于 f 下方的曲线则不属于 f-dp。符合 f-dp 的权衡函数,从图中可以看出,当 I 类错误固定时,II 类错误的概率高于 f,也就更难区分 P 和 Q 了。
在进一步讨论之前,我们根据上述的定义可以给出一个更严格的界限,如下所示:
令机制 M 符合 f-dp,对于任意的 α ∈[0,1],定义:
f − 1 ( α ) : = i n f { t ∈ [ 0 , 1 ] : f ( t ) ≤ α } f S = m a x { f , f − 1 } f^{-1}(\alpha):=inf\{t\in[0,1]:f(t)\leq\alpha\}\\ f^S=max\{f,f^{-1}\} f − 1 ( α ) := in f { t ∈ [ 0 , 1 ] : f ( t ) ≤ α } f S = ma x { f , f − 1 } 则 M 符合 f S − D P f^S-DP f S − D P f S − D P f^S-DP f S − D P
f S = m a x { f , f − 1 } ≥ f f^S = max\{ f, f^{-1} \} ≥ f f S = ma x { f , f − 1 } ≥ f
f S = ( f S ) − 1 f^S = (f^S)^{-1} f S = ( f S ) − 1
这里注意到 f − 1 = T ( Q , P ) f^{-1} = T(Q,P) f − 1 = T ( Q , P ) f S − d p f^S-dp f S − d p
证明过程暂时省略,此处仅作占位
至此,我们给出了 f-dp 的定义和其图形意义。接下来我们关注的,是 f − d p f-dp f − d p ( ε , δ ) − d p (ε, δ)-dp ( ε , δ ) − d p
四、f − d p f-dp f − d p ( ϵ , δ ) − d p (\epsilon, \delta)-dp ( ϵ , δ ) − d p # 4.1 f − d p f-dp f − d p ( ε , δ ) − d p (ε, δ)-dp ( ε , δ ) − d p # 这里直接给出对应的表达式:
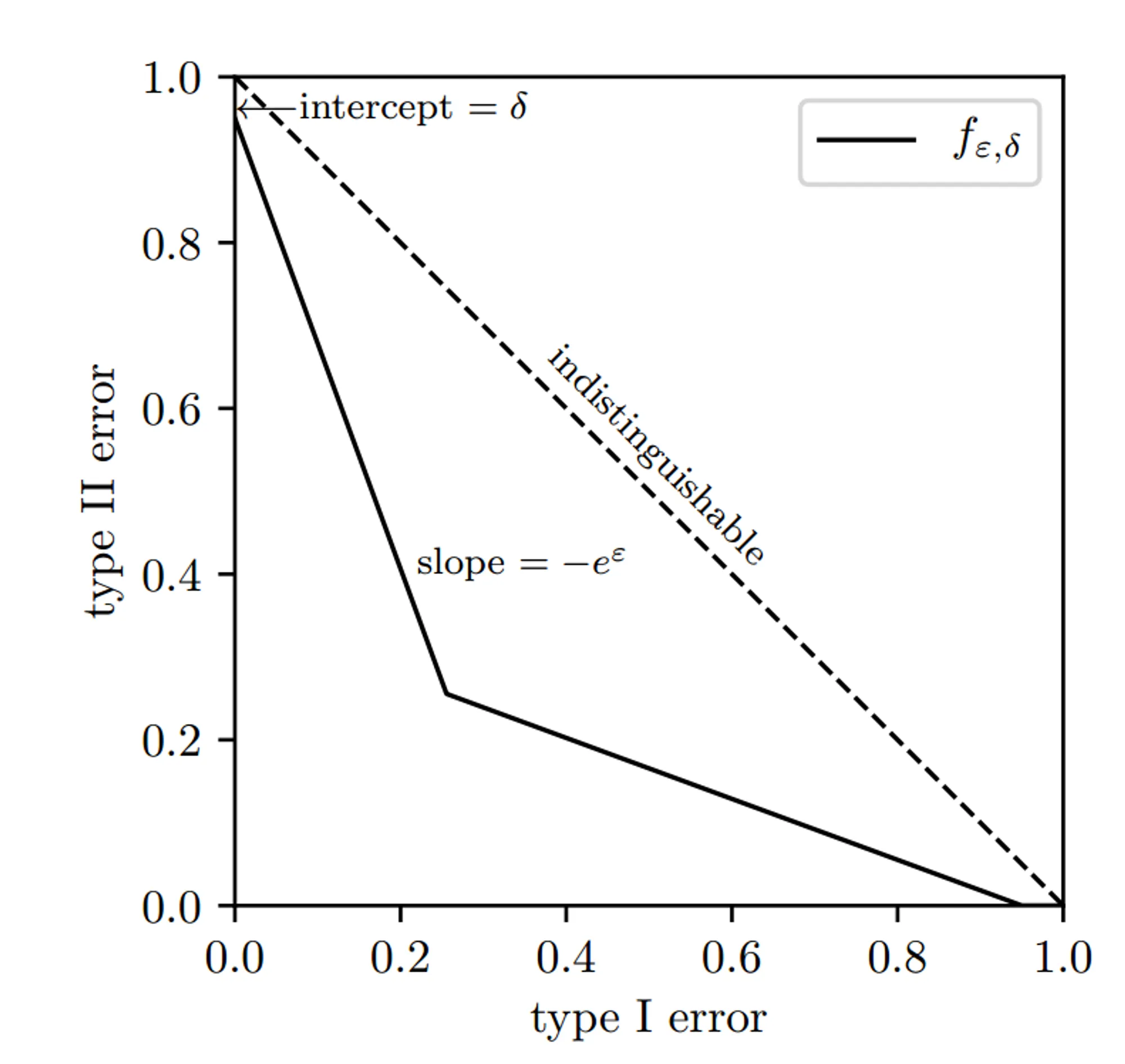
f ϵ , δ ( α ) = m a x { 0 , 1 − δ − e ϵ α , e − ϵ ( 1 − δ − α ) } f_{\epsilon,\delta}(\alpha)=max\{0,1-\delta-e^\epsilon\alpha,e^{-\epsilon}(1-\delta-\alpha)\} f ϵ , δ ( α ) = ma x { 0 , 1 − δ − e ϵ α , e − ϵ ( 1 − δ − α )} 其函数图像为:
对照上面给出的充要条件,f ε , δ f_{ε, δ} f ε , δ f ε , δ f_{ε, δ} f ε , δ T ( M ( S ) , M ( S ’ ) ) ≥ f ε , δ T(M(S), M(S’)) ≥ f_{ε, δ} T ( M ( S ) , M ( S ’ )) ≥ f ε , δ
4.2 高斯机制的定义# 接下来我们将着重考虑 dp 中比较关键的 “高斯机制” 的表达形式。这里直接给出其表达式:
G μ : = T ( N ( 0 , 1 ) , N ( μ , 1 ) ) G_\mu:=T(N(0,1),N(\mu,1)) G μ := T ( N ( 0 , 1 ) , N ( μ , 1 )) 也就是说,μ-GDP 的表现,直观上来讲就是鉴别 N(0, 1) 和 N(μ, 1) 的难易程度。我们还可以给出一个更直观的表达式:
G μ ( α ) = Φ ( Φ − 1 ( 1 − α ) − μ ) G_\mu(\alpha)=\Phi(\Phi^{-1}(1-\alpha)-\mu) G μ ( α ) = Φ ( Φ − 1 ( 1 − α ) − μ ) 其中,Φ 是标准正态分布的累积密度函数,对于一般的正态分布,其累计密度函数如下,其中 erf() 为误差函数:
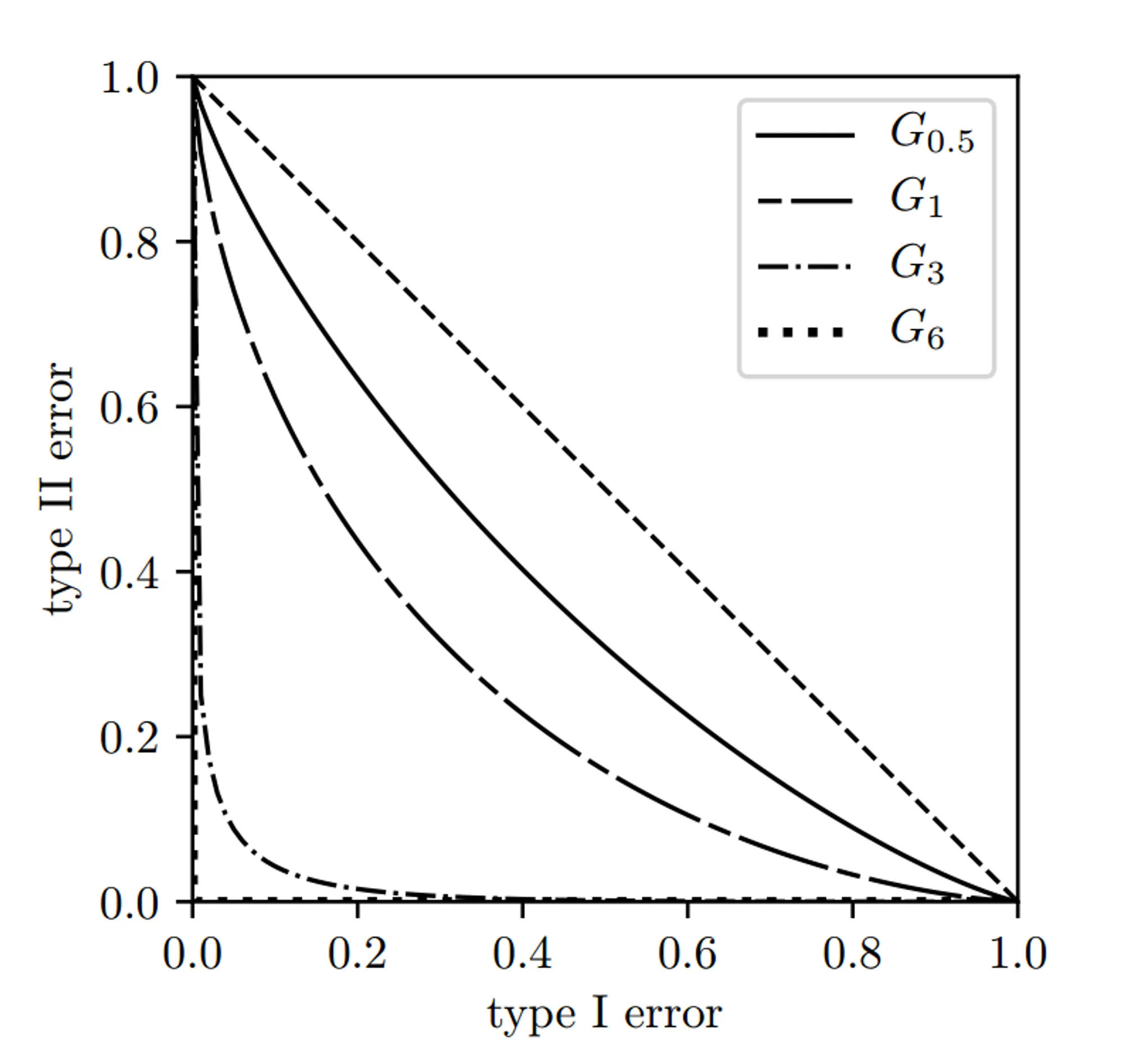
Φ ( x ) = 1 2 [ 1 + e r f ( x − μ σ 2 ) ] \Phi(x)=\frac{1}{2}[1+erf(\frac{x-\mu}{\sigma \sqrt{2}})] Φ ( x ) = 2 1 [ 1 + er f ( σ 2 x − μ )] 由其表达式可以看出,当 α 固定时,值随着 μ 的增加而递减。如下图所示:
我们现在了解了 G μ − D P G_μ-DP G μ − D P t r a d e − o f f trade-off t r a d e − o ff
① G μ − D P G_μ-DP G μ − D P
② G μ − D P G_μ-DP G μ − D P ( ε , δ ) − D P (ε, δ)-DP ( ε , δ ) − D P
③ G μ − D P G_μ-DP G μ − D P
首先,同样给出 μ-GDP 的定义。机制M,如果对于任意的邻近数据集 S 和 S‘,均有:
T ( M ( S ) , M ( S ′ ) ) ≥ G μ T(M(S),M(S')) \geq G_\mu T ( M ( S ) , M ( S ′ )) ≥ G μ 则称:机制 M 符合 μ-GDP。
这个定义的好处在于它的隐私保护意义是相当直观的。如上图所示,μ越大,相同 I 类错误 α 的前提下,II 类错误 β 就越小,攻击者就越容易分辨 S 和 S’,隐私保护的能力就越弱。
接下来考虑“高斯机制”的加噪方式。
4.3 添加高斯噪声# 首先定义敏感度:
s e n s ( θ ) = s u p S , S ′ ∣ θ ( S ) − θ ( S ′ ) ∣ sens(\theta)=sup_{S,S'}|\theta(S)-\theta(S')| se n s ( θ ) = s u p S , S ′ ∣ θ ( S ) − θ ( S ′ ) ∣ 这里 θ 是要进行隐私分析考察的统计量,敏感度为全局敏感度。高斯机制是通过向统计量 θ 上添加高斯噪声,来模糊其从属 S 还是 S’。也就是说:
M ( S ) = θ ( S ) + ξ , ξ ∼ N ( 0 , s e n s ( θ ) 2 / μ 2 ) M(S)=\theta(S)+\xi, \;\;\xi\sim N(0,sens(\theta)^2/\mu^2) M ( S ) = θ ( S ) + ξ , ξ ∼ N ( 0 , se n s ( θ ) 2 / μ 2 ) 则 M 符合 μ-GDP。其证明过程如下所示:
T ( M ( S ) , M ( S ′ ) ) = G ∣ θ ( S ) − θ ( s ′ ) ∣ / σ ≥ G μ T(M(S),M(S'))=G_{|\theta(S)-\theta(s')|/\sigma}\geq G_\mu T ( M ( S ) , M ( S ′ )) = G ∣ θ ( S ) − θ ( s ′ ) ∣/ σ ≥ G μ l e t σ 2 = s e n s ( θ ) 2 / μ 2 , T ( M ( S ) , M ( S ′ ) ) = T ( N ( θ ( S ) , σ 2 ) , N ( θ ( S ′ ) , σ 2 ) let\; \sigma^2=sens(\theta)^2/\mu^2,\;\;T(M(S),M(S'))=T(N(\theta(S),\sigma^2),N(\theta(S'),\sigma^2) l e t σ 2 = se n s ( θ ) 2 / μ 2 , T ( M ( S ) , M ( S ′ )) = T ( N ( θ ( S ) , σ 2 ) , N ( θ ( S ′ ) , σ 2 ) 在正态分布中,通过 z = x − μ σ z=\frac{x-\mu}{\sigma} z = σ x − μ N ( θ ( S ) , σ 2 ) N(\theta(S),\sigma^2) N ( θ ( S ) , σ 2 ) N ( θ ( S ) , σ 2 ) N(\theta(S),\sigma^2) N ( θ ( S ) , σ 2 ) N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) N ( θ ( S ′ ) , σ 2 ) N(\theta(S'),\sigma^2) N ( θ ( S ′ ) , σ 2 ) N ( θ ( S ’ ) − θ ( S ) σ , 1 ) N(\frac{\theta(S’)-\theta(S)}{\sigma},1) N ( σ θ ( S ’ ) − θ ( S ) , 1 )
T ( M ( S ) , M ( S ′ ) ) = T ( N ( θ ( S ) , σ 2 ) , N ( θ ( S ′ ) , σ 2 ) = G ∣ θ ( S ) − θ ( s ′ ) ∣ / σ T(M(S),M(S'))=T(N(\theta(S),\sigma^2),N(\theta(S'),\sigma^2)=G_{|\theta(S)-\theta(s')|/\sigma} T ( M ( S ) , M ( S ′ )) = T ( N ( θ ( S ) , σ 2 ) , N ( θ ( S ′ ) , σ 2 ) = G ∣ θ ( S ) − θ ( s ′ ) ∣/ σ 又因为:
∣ θ ( S ) − θ ( s ′ ) ∣ / σ ≤ s e n s ( θ ) / σ = μ |\theta(S)-\theta(s')|/\sigma \leq sens(\theta)/\sigma=\mu ∣ θ ( S ) − θ ( s ′ ) ∣/ σ ≤ se n s ( θ ) / σ = μ 根据 μ-GDP 的递减性质,可以得到:
综上,符合 μ-GDP 隐私保护,证毕。
4.4 后处理性质# 如果机制 M 符合 f-DP,那么它的后处理过程也符合 f-dp。
4.5 高斯机制和 (ε, δ)-dp 之间的转换关系# 机制 M 是 μ-GDP,当且仅当它符合 (ε, δ(ε) )-DP,这里有:
δ ( ϵ ) = Φ ( − ϵ μ + μ 2 ) − e ϵ Φ ( − ϵ μ − μ 2 ) , ϵ ≥ 0 \delta(\epsilon)=\Phi(-\frac{\epsilon}{\mu}+\frac{\mu}{2})-e^\epsilon \Phi(-\frac{\epsilon}{\mu}-\frac{\mu}{2}),\;\;\epsilon\geq 0 δ ( ϵ ) = Φ ( − μ ϵ + 2 μ ) − e ϵ Φ ( − μ ϵ − 2 μ ) , ϵ ≥ 0 4.6 组隐私# 这里需要对“组隐私”(Group Privacy)的概念做个定义。这里暂时还没有涉及到后续的“组合定理”,考察的仍旧是单次查询的隐私保护。假设存在一系列的数据集:S=S0, S1, S2, …, Sk = S’, k ≥ 2, 且 Si 和 Si+1 是临近数据集。我们说 S 和 S’ 是 k-邻近数据集,也就是说, S 和 S‘ 之间最多有 k 个不同个体的差异。
对于规模为 k 的组,机制 M 符合 f - DP, 如果对于所有的 k-邻近数据集 S 和 S’,都有:
T ( M ( S ) , M ( S ′ ) ) ≥ f T(M(S),M(S'))\geq f T ( M ( S ) , M ( S ′ )) ≥ f 反过来,如果一个机制是 f − D P f-DP f − D P [ 1 − ( 1 − f ) ∘ k ] − D P [1-(1-f)^{\circ k}]-DP [ 1 − ( 1 − f ) ∘ k ] − D P
( 1 − f ) ∘ 1 = ( 1 − f ) , ( 1 − f ) ∘ 2 = 1 − f ( 1 − f ( x ) ) , . . . (1-f)^{\circ 1}=(1-f),\;\;(1-f)^{\circ 2}=1-f(1-f(x)),... ( 1 − f ) ∘ 1 = ( 1 − f ) , ( 1 − f ) ∘ 2 = 1 − f ( 1 − f ( x )) , ... 如果一个机制是 μ − G D P \mu-GDP μ − G D P k μ − G D P k\mu-GDP k μ − G D P
这里有一个有趣的地方,令 μ ≥ 0 μ ≥ 0 μ ≥ 0 ε = μ / k , ε = \mu /k, ε = μ / k ,
1 − ( 1 − f ϵ , 0 ) ∘ k → T ( L a p ( 0 , 1 ) , L a p ( μ , 1 ) ) 1-(1-f_{\epsilon,0})^{\circ k}\rightarrow T(Lap(0,1),Lap(\mu,1)) 1 − ( 1 − f ϵ , 0 ) ∘ k → T ( L a p ( 0 , 1 ) , L a p ( μ , 1 )) 这个近似是比较准确的,即使当 k 很小的时候,精度也比较高。
五、组合定理# 设 X 为 数据集空间,n 为组合中的机制数量。令 M 1 : X → Y 1 M_1: X \rightarrow Y_1 M 1 : X → Y 1 M 2 : X × Y 1 → Y 2 M_2: X × Y_1 \rightarrow Y_2 M 2 : X × Y 1 → Y 2 M 2 M_2 M 2 M 1 M_1 M 1 M : X → Y 1 × Y 2 M:X \rightarrow Y_1 × Y_2 M : X → Y 1 × Y 2
M ( S ) = ( y 1 , M 2 ( S , y 1 ) ) , y 1 = M 1 ( S ) M(S)=(y_1,M_2(S,y_1)),\;\; y_1=M_1(S) M ( S ) = ( y 1 , M 2 ( S , y 1 )) , y 1 = M 1 ( S ) 显然,这样的组合是可以不断递归下去的。总的来说,给定一系列的机制 M i : X × Y 1 × Y 2 × Y 3 … × Y i − 1 → Y i M_i : X × Y_1 × Y_2× Y_3…× Y_i-1 \rightarrow Y_i M i : X × Y 1 × Y 2 × Y 3 … × Y i − 1 → Y i
M : X → Y 1 × Y 2 × . . . Y n M:X\rightarrow Y_1× Y_2×... Y_n M : X → Y 1 × Y 2 × ... Y n 这种类马尔可夫链的形式,使得我们可以直接运用相关的数学工具来进行分析。
5.1 一般组合定理# 考虑两个权衡函数 f 和 g,对于一些概率分布 P , P ’ , Q , Q ’ P, P’, Q, Q’ P , P ’ , Q , Q ’ f = T ( P , Q ) , g = T ( P ’ , Q ’ ) f = T(P,Q),g = T(P’,Q’) f = T ( P , Q ) , g = T ( P ’ , Q ’ )
f ⊗ g : = T ( P × P ′ , Q × Q ′ ) f \otimes g:=T(P\times P',Q\times Q') f ⊗ g := T ( P × P ′ , Q × Q ′ ) 根据作者的证明,f ⊗ g f \otimes g f ⊗ g
⊗ \otimes ⊗
如果有 g 1 ≥ g 2 g_1≥g_2 g 1 ≥ g 2 f ⊗ g 1 ≥ f ⊗ g 2 f \otimes g_1 ≥ f \otimes g_2 f ⊗ g 1 ≥ f ⊗ g 2
f ⊗ I d = I d ⊗ f f \otimes Id = Id \otimes f f ⊗ I d = I d ⊗ f I d ( x ) = 1 − x , 0 ≤ x ≤ 1 Id(x)=1-x, 0≤x≤1 I d ( x ) = 1 − x , 0 ≤ x ≤ 1
( f ⊗ g ) − 1 = f − 1 ⊗ g − 1 (f \otimes g)^{-1} = f^{-1} \otimes g^{-1} ( f ⊗ g ) − 1 = f − 1 ⊗ g − 1
当然,I d Id I d 同分布的权衡函数。给定了张量积的定义后,我 们就可以给出一般组合定理了:
令 M i ( ⋅ , y 1 , … , y i − 1 ) M_i(·, y_1, …, y_{i-1}) M i ( ⋅, y 1 , … , y i − 1 ) y 1 ∈ Y 1 , … , y i − 1 ∈ Y i − 1 y_1 \in Y_1, …, y_{i-1} \in Y_{i-1} y 1 ∈ Y 1 , … , y i − 1 ∈ Y i − 1 f i − D P f_i-DP f i − D P
M : X → Y 1 × Y 2 × . . . Y i − 1 i s f 1 ⊗ f 2 ⊗ . . . f n − D P M: X\rightarrow Y_1\times Y_2\times ...Y_{i-1} \;\;is\;\; f_1 \otimes f_2\otimes ...f_{n}-DP M : X → Y 1 × Y 2 × ... Y i − 1 i s f 1 ⊗ f 2 ⊗ ... f n − D P 这个定理符合①封闭性;②严紧性。封闭性表现在,n个 f-dp 机制的组合,仍旧符合 dp 规范。严紧性表现在,给出的这个 f 1 ⊗ f 2 ⊗ . . . f n − D P f_1 \otimes f_2\otimes ...f_{n}-DP f 1 ⊗ f 2 ⊗ ... f n − D P
特别的,对于高斯机制的 GDP 而言,组合定理相当简单:
G μ 1 ⊗ G μ 2 ⊗ . . . G μ n = G μ , μ = μ 1 2 + μ 2 2 + . . . + μ n 2 G_{\mu_1} \otimes G_{\mu_2} \otimes... \;G_{\mu_n}=G_{\mu},\;\; \mu=\sqrt{\mu_1^2+\mu_2^2+...+\mu_n^2} G μ 1 ⊗ G μ 2 ⊗ ... G μ n = G μ , μ = μ 1 2 + μ 2 2 + ... + μ n 2 因此,n 个 μ i − G D P \mu_i-GDP μ i − G D P μ 1 2 + μ 2 2 + . . . + μ n 2 − G D P \sqrt{\mu_1^2+\mu_2^2+...+\mu_n^2}-GDP μ 1 2 + μ 2 2 + ... + μ n 2 − G D P
5.2 中心极限定理# 研究中心极限定理的目的在于,虽然高斯机制下的最终组合表达式是简单的、明了的,但是对于一般的 f i − D P f_i-DP f i − D P
中心极限定理的概念是:在许多情况下,对于独立并同样分布的随机变量,即使原始变量本身不是正态分布,标准化样本均值的抽样分布也趋向于标准正态分布。我们可以通过这个方法,来求出张量积 f 1 ⊗ f 2 ⊗ . . . f n − D P f_1 \otimes f_2\otimes ...f_{n}-DP f 1 ⊗ f 2 ⊗ ... f n − D P
这里引入四个泛函:
k l ( f ) : = − ∫ 0 1 l o g ∣ f ′ ( x ) ∣ d x κ 2 ( f ) : = ∫ 0 1 l o g 2 ∣ f ′ ( x ) ∣ d x κ 3 ( f ) : = ∫ 0 1 ∣ l o g ∣ f ′ ( x ) ∣ ∣ 3 d x κ 3 ‾ : = ∫ 0 1 ∣ l o g ∣ f ′ ( x ) ∣ + k l ( f ) ∣ 3 d x kl(f):=-\int_0^1 log|f'(x)|dx\\ \kappa_2(f):=\int_0^1log^2|f'(x)|dx\\ \kappa_3(f):=\int_0^1|log|f'(x)||^3dx\\ \overline{\kappa_3}:=\int_0^1|log|f'(x)|+kl(f)|^3dx k l ( f ) := − ∫ 0 1 l o g ∣ f ′ ( x ) ∣ d x κ 2 ( f ) := ∫ 0 1 l o g 2 ∣ f ′ ( x ) ∣ d x κ 3 ( f ) := ∫ 0 1 ∣ l o g ∣ f ′ ( x ) ∣ ∣ 3 d x κ 3 := ∫ 0 1 ∣ l o g ∣ f ′ ( x ) ∣ + k l ( f ) ∣ 3 d x 令 f 1 , … , f n f_1,…,f_n f 1 , … , f n κ 3 ( f i ) < ∞ \kappa_3(f_i)<\infin κ 3 ( f i ) < ∞ 1 ≤ i ≤ n 1≤i≤n 1 ≤ i ≤ n
μ : = 2 ∣ ∣ k l ∣ ∣ 1 ∣ ∣ κ 2 ∣ ∣ 1 − ∣ ∣ k l ∣ ∣ 2 2 , γ : = 0.56 ∣ ∣ κ 3 ‾ ∣ ∣ 1 ( ∣ ∣ κ 2 ∣ ∣ 1 − ∣ ∣ k l ∣ ∣ 2 2 ) 3 / 2 \mu:=\frac{2||kl||_1}{\sqrt{||\kappa_2||_1-||kl||_2^2}},\gamma:=\frac{0.56||\overline{\kappa_3}||_1}{(||\kappa_2||_1-||kl||_2^2)^{3/2}} μ := ∣∣ κ 2 ∣ ∣ 1 − ∣∣ k l ∣ ∣ 2 2 2∣∣ k l ∣ ∣ 1 , γ := ( ∣∣ κ 2 ∣ ∣ 1 − ∣∣ k l ∣ ∣ 2 2 ) 3/2 0.56∣∣ κ 3 ∣ ∣ 1 假设 γ < 1 / 2 \gamma < 1/2 γ < 1/2 α ∈ [ γ , 1 − γ ] \alpha \in [\gamma, 1-\gamma] α ∈ [ γ , 1 − γ ]
G μ ( α + γ ) − γ ≤ f 1 ⊗ f 2 ⊗ . . . ⊗ f n ( α ) ≤ G μ ( α − γ ) + γ G_\mu(\alpha+\gamma)-\gamma \leq f_1 \otimes f_2\otimes...\otimes f_n(\alpha) \leq G_\mu(\alpha-\gamma)+\gamma G μ ( α + γ ) − γ ≤ f 1 ⊗ f 2 ⊗ ... ⊗ f n ( α ) ≤ G μ ( α − γ ) + γ 当n 趋向于无穷时,可以得到以下近似:
lim n → ∞ f n 1 ⊗ f n 2 ⊗ . . . f n n ( α ) = G 2 K / s ( α ) , w i t h ∑ i = 1 n k l ( f n i ) → K ; ∑ i = 1 n κ 2 ( f n i ) → s 2 \lim_{n\rightarrow \infin}f_{n1}\otimes f_{n2}\otimes...f_{nn}(\alpha)=G_{2K/s}(\alpha), with \; \sum_{i=1}^{n}kl(f_{ni})\rightarrow K;\sum_{i=1}^n\kappa_2(f_{ni})\rightarrow s^2 n → ∞ lim f n 1 ⊗ f n 2 ⊗ ... f nn ( α ) = G 2 K / s ( α ) , w i t h i = 1 ∑ n k l ( f ni ) → K ; i = 1 ∑ n κ 2 ( f ni ) → s 2 5.3 对 (ε, δ)-DP 的近似# 首先改写最终的表达式:
f ϵ 1 , δ 1 ⊗ f ϵ 2 , δ 2 ⊗ . . . ⊗ f ϵ n , δ n ( α ) f_{\epsilon_1,\delta_1} \otimes f_{\epsilon_2,\delta_2}\otimes...\otimes f_{\epsilon_n,\delta_n}(\alpha) f ϵ 1 , δ 1 ⊗ f ϵ 2 , δ 2 ⊗ ... ⊗ f ϵ n , δ n ( α ) 考虑张量积的形式,可以改写为:
f ϵ , δ = f ϵ , 0 ⊗ f 0 , δ f_{\epsilon,\delta}=f_{\epsilon,0}\otimes f_{0,\delta} f ϵ , δ = f ϵ , 0 ⊗ f 0 , δ 进而有:
f ϵ 1 , δ 1 ⊗ . . . ⊗ f ϵ n , δ n = ( f ϵ 1 , 0 ⊗ . . . ⊗ f ϵ n , 0 ) ⊗ ( f 0 , δ 1 ⊗ . . . ⊗ f 0 , δ n ) f_{\epsilon1,\delta_1} \otimes ...\otimes f_{\epsilon_n,\delta_n}=(f_{\epsilon_1,0}\otimes...\otimes f_{\epsilon_n,0})\otimes(f_{0,\delta_1}\otimes...\otimes f_{0,\delta_n}) f ϵ 1 , δ 1 ⊗ ... ⊗ f ϵ n , δ n = ( f ϵ 1 , 0 ⊗ ... ⊗ f ϵ n , 0 ) ⊗ ( f 0 , δ 1 ⊗ ... ⊗ f 0 , δ n ) 前者套用上面的结论,近似为 G ϵ 1 2 + … + ϵ n 2 G_{\sqrt{\epsilon_1^2+…+\epsilon_n^2}} G ϵ 1 2 + … + ϵ n 2 f 0 , 1 − ( 1 − δ 1 ) ( 1 − δ 2 ) … ( 1 − δ n ) f_{0,1-(1-\delta_1)(1-\delta_2)…(1-\delta_n)} f 0 , 1 − ( 1 − δ 1 ) ( 1 − δ 2 ) … ( 1 − δ n )
∑ i = 1 n ϵ n i 2 → μ 2 , max 1 ≤ i ≤ n ϵ n i → 0 , ∑ i = 1 n δ n i → δ , max 1 ≤ i ≤ n δ n i → 0 \sum_{i=1}^n\epsilon_{ni}^2\rightarrow\mu^2, \max_{1\leq i \leq n}\epsilon_{ni}\rightarrow 0,\sum_{i=1}^n\delta_{ni}\rightarrow \delta, \max_{1\leq i \leq n}\delta_{ni}\rightarrow0 i = 1 ∑ n ϵ ni 2 → μ 2 , 1 ≤ i ≤ n max ϵ ni → 0 , i = 1 ∑ n δ ni → δ , 1 ≤ i ≤ n max δ ni → 0 有:
f ϵ n 1 , δ n , 1 ⊗ . . . ⊗ f ϵ n n , δ n n → G μ ⊗ f 0 , 1 − e − δ f_{\epsilon_{n1},\delta_{n,1}}\otimes ...\otimes f_{\epsilon_{nn},\delta_{nn}} \rightarrow G_{\mu} \otimes f_{0,1-e^{-\delta}} f ϵ n 1 , δ n , 1 ⊗ ... ⊗ f ϵ nn , δ nn → G μ ⊗ f 0 , 1 − e − δ 六、整理# f − D P f-DP f − D P ( ε , δ ) − D P (ε, δ)-DP ( ε , δ ) − D P 思想 T r a d e − O f f : T ( P , Q ) ( α ) = i n f { β Φ : α Φ ≤ α } Trade-Off : T(P,Q)(\alpha) = inf \{ \beta_\Phi : \alpha_\Phi \leq \alpha \} T r a d e − O ff : T ( P , Q ) ( α ) = in f { β Φ : α Φ ≤ α } $KL-Divergence : D_{KL}(P| 公式 i f : T ( M ( S ) , M ( S ’ ) ) ≥ f f o r a l l n e i g h b o r i n g S a n d S ′ t h e n M i s f − d p if\;:\; T(M(S),M(S’)) \geq f \;for\; all\; neighboring\; S\;and\;S'\\then\;M\;is\;f-dp\; i f : T ( M ( S ) , M ( S ’ )) ≥ f f or a ll n e i g hb or in g S an d S ′ t h e n M i s f − d p i f : P ( M ( S ) ∈ E ) ≤ e ϵ P [ M ( S ’ ) ∈ E ] + δ f o r a l l n e i g h b o r i n g S a n d S ′ t h e n M i s ( ϵ , δ ) − D P if:P(M(S)\in E)\leq e^\epsilon P[M(S’)\in E]+\delta\; for \; all\;neighboring\;S\;and\;S'\\then\; M \; is\; (\epsilon,\delta)-DP i f : P ( M ( S ) ∈ E ) ≤ e ϵ P [ M ( S ’ ) ∈ E ] + δ f or a ll n e i g hb or in g S an d S ′ t h e n M i s ( ϵ , δ ) − D P 转化 f ϵ , δ ( α ) = m a x { 0 , 1 − δ − e ϵ α , e − ϵ ( 1 − δ − α ) } f_{\epsilon, \delta}(\alpha)=max\{ 0,1-\delta-e^\epsilon\alpha,e^{-\epsilon}(1-\delta-\alpha) \} f ϵ , δ ( α ) = ma x { 0 , 1 − δ − e ϵ α , e − ϵ ( 1 − δ − α )} 高斯机制(定义) G μ : = T ( N ( 0 , 1 ) , N ( μ , 1 ) ) G μ ( α ) = Φ ( Φ − 1 ( 1 − α ) − μ ) ,随着 μ 增加而保护性递减 M i s μ − G D P i f : T ( M ( S ) , M ( S ′ ) ) ≥ G μ G_\mu := T(N(0,1),N(\mu,1))\\G_\mu(\alpha)=\Phi(\Phi^{-1}(1-\alpha)-\mu),随着 μ 增加而保护性递减\\M\;is\; \mu-GDP\;if\;:T(M(S),M(S'))\geq G_\mu G μ := T ( N ( 0 , 1 ) , N ( μ , 1 )) G μ ( α ) = Φ ( Φ − 1 ( 1 − α ) − μ ) ,随着 μ 增加而保护性递减 M i s μ − G D P i f : T ( M ( S ) , M ( S ′ )) ≥ G μ 高斯机制(加噪) M ( S ) = θ ( S ) + ξ , ξ ∼ N ( 0 , s e n s ( θ ) 2 / μ 2 ) t h e n M i s μ − G D P M(S)=\theta(S)+\xi, \xi \sim N(0,sens(\theta)^2/\mu^2)\\then \; M\; is\; \mu-GDP M ( S ) = θ ( S ) + ξ , ξ ∼ N ( 0 , se n s ( θ ) 2 / μ 2 ) t h e n M i s μ − G D P M ( S ) = θ ( S ) + ξ , ξ ∼ N ( 0 , 2 s e n s ( θ ) 2 l o g ( 1.25 / δ ) ϵ 2 ) t h e n M i s ( ϵ , δ ) − D P M(S)=\theta(S)+\xi, \xi \sim N(0,\frac{2sens(\theta)^2log(1.25/\delta)}{\epsilon^2})\\then\;M\;is\; (\epsilon,\delta)-DP M ( S ) = θ ( S ) + ξ , ξ ∼ N ( 0 , ϵ 2 2 se n s ( θ ) 2 l o g ( 1.25/ δ ) ) t h e n M i s ( ϵ , δ ) − D P 转化(高斯机制) i f M i s ( ϵ , δ ( ϵ ) ) − D P f o r a l l ϵ ≥ 0 , a n d δ ( ϵ ) = Φ ( − ϵ μ + μ 2 ) − e ϵ Φ ( − ϵ μ − μ 2 ) t h e n M i s μ − G D P if\; M\; is\; (\epsilon,\delta(\epsilon))-DP\;for\;all\;\epsilon \geq 0,\;and \\\delta(\epsilon)=\Phi(-\frac{\epsilon}{\mu}+\frac{\mu}{2})-e^\epsilon\Phi(-\frac{\epsilon}{\mu}-\frac{\mu}{2})\\then\; M\;is\;\mu-GDP i f M i s ( ϵ , δ ( ϵ )) − D P f or a ll ϵ ≥ 0 , an d δ ( ϵ ) = Φ ( − μ ϵ + 2 μ ) − e ϵ Φ ( − μ ϵ − 2 μ ) t h e n M i s μ − G D P 组合 G μ 1 ⊗ … ⊗ G μ n = G μ , μ = μ 1 2 + … + μ n 2 G_{\mu_1}\otimes …\otimes G_{\mu_n}=G_\mu,\;\mu=\sqrt{\mu_1^2+…+\mu_n^2} G μ 1 ⊗ … ⊗ G μ n = G μ , μ = μ 1 2 + … + μ n 2 M o m e n t A c c o u n t a n t R n e y i A c c o u n t a n t … … Moment\;Accountant\\Rneyi\;Accountant\\…… M o m e n t A cco u n t an t R n ey i A cco u n t an t ……