一、任务说明#

• 总结本周学习的三篇论文主要内容；

• 汇总论文中出现过的知识点、方法、技巧；

• 整理疏通各自的方法流程；

• 以上部分存放在“知识字典”段落里

• 对相关的公式进行推导、整理；

• 对尚且存在疑问的部分进行规范的整理

• 以上部分存放在“解释疑问”段落里

二、知识字典#

2.1 主要内容概要#

2-1-Deep Learning with Differential Privacy(CCS)#

• 作者： Martin Abadi, Andy Chu, lan Goodfellow, 等

• 场景：深度学习需要大量的数据，这会涉及到很多的众包、敏感数据。因此需要设计一种技术来满足隐私保证的需求。

• 问题：现有的方案包含如下不足：①很大程度依赖于凸函数，缺乏对非凸函数的解决方法；②对复杂神经网络会造成过大的隐私损失；③使用的“强组合定理”是基于“损失函数期望的范围”来规定隐私成本的上界的，这个上界并不“紧”。

• 方案：运用随机梯度下降算法(SGD)，每次计算损失函数的梯度后，根据指定的标准对梯度进行裁剪，然后往梯度中加入高斯噪声。下次更新参数时，就把θ减去学习率和梯度乘积的值。为了对算法的隐私损失提供更紧的估计，作者还使用了“矩统计”的方法。

• 效果：在满足(8,10^{-5})-差分隐私的条件下，MNIST数据集的准确率达97%，CIFAR-10数据集的准确率达73%，和非隐私保护的基线情况相比，MNIST数据集准确率相差约1.3%，而CIFAR-10的准确率则相差约7%，因此可以做出如下总结：①解决了算法对非凸函数的支持问题；②减少了隐私成本；③使用矩统计方法获得了更紧的隐私成本上界；④对于更加复杂的模型(CIFAR-10)，差分隐私版本的算法精确度还偏低。

2-2-Differentially Private Generative Adversarial Network#

• 作者： Liyang Xie, Kaixiang Lin, Shu Wang, 等

• 场景：GAN及其衍生算法生成的样本，在深度学习的高复杂度网络下，其分布往往会聚集在训练数据集的周围，当涉及到隐私数据时，攻击者只需要通过重复采样，便有很大的概率恢复隐私数据。

• 问题：算法既需要关注生成样本的质量，还需要确保符合隐私保护的标准。现有的GAN算法使用的是JS-距离，并且在深度学习模型中往往裁剪的是权重值。

• 方案：主要采用了“生成对抗网络”(GAN)思想，同时训练两个模型，一个是生成模型G，一个是判别模型D。前者将输入分布转化成近似于数据分布的输出分布，后者用于估计一个样本来自于训练数据集而非输出集G的可能性。在训练时，主要将噪声和梯度裁剪结合，同时使用Wasserstein距离来代替GAN中的JS-发散。主要解决“GAN会隐式地披露隐私数据”、“梯度失真”、“隐私损失和公共数据集里需要标记的数量成正比”等问题。

• 效果：作者证明了在裁剪权重的同时，梯度也同样可以被约束住，这避免了梯度上不必要的失真。作者使用了Wasserstein距离来代替JS距离，不仅仅保留了Lipschitz property的损失函数，还提供了足够的隐私保证。区别于隐私保护深度学习框架（隐私损失与公共数据集里需要标记的数量成正比），DPGAN的隐私损失与与生成的数据量无关。

2-3-Differentially-Private Deep Learning from an Optimization Perspective#

• 作者： Liyao Xiang, Jingbo Yang, Baochun Li

• 场景：过去的隐私保护策略是以牺牲学习性能为前提的。作者认为产生这个问题的根本原因在于“模型效用”和“数据隐私”之间的关系没有被准确识别，导致隐私约束过于严格。

• 问题：当差分隐私的机制将噪声添加到模型参数中时，随着隐私要求变得严格，学习结果的效用会显著降低，即使使用矩统计已经显著改善了强组合的效用，问题仍旧没有彻底解决。

• 方案：采用了优化思想，着重探讨了不同参数扰动对于隐私成本的影响大小，从而得出加噪的方向。为了使得成体的成本最小化，应该根据成本函数的最小敏感度方向来选取噪声分布z(而这个方向是由所有参数对于训练样本成本函数的导数向量w来决定的)。主要的工作在于公式的推导和证明。

• 效果：经过对比，隐私成本越低，隐私要求越严格，作者方法的精确度相比高斯机制的优势就越大。在MNIST, SVHN和CIFAR-10数据集上，作者的隐私机制在各自等级的隐私约束下都提高了模型的精确度，尤其是在隐私成本很低、隐私要求很高的情况下。

2.2 知识点整理#

2.2.1 深度学习#

        让计算机模拟人类的认知过程，从经验中学习，根据层次化的概念体系来理解世界。其中最突出的特点是“神经网络的层次”很“深”。深度的网络能够有着强悍的拟合能力，但有时候也会产生过拟合以及陷入局部最优解的困境中，为了解决这些问题，需要根据多种优化算法来避免这些问题。

        常用的深度学习模型有：

• 卷积神经网络(CNN)，使用卷积来替代一般的矩阵乘法运算的神经网络

• 循环神经网络和递归神经网络(RNN)，处理序列问题和学习推论

• 自编码器，特征表达和数据降维

• 生成式对抗网络，从训练样本中学习出新样本

2.2.2 组合定理#

        组合定理想要探讨的问题是：如何将一系列满足差分隐私的查询组合在一起，使得整体仍旧满足差分隐私？

        例如，对于一个三层神经网络，如果将每个神经元计算梯度看成一个查询函数$\nabla f:D\rightarrow g$，输入数据集D，输出梯度g。那么组合定理研究的就是整个神经网络满足怎样的差分隐私。

        组合定理包含两个部分的内容：

• 基本组成原理：不考虑查询函数之间的关联性（查询互相独立）

• 高级组成原理：考虑查询函数之间的关联性

        先来探究一下**隐私损失(Privacy Loss)**的概念：

        我们用M来表示一系列满足差分隐私的查询机制，数量为k。M_k 表示第i个查询机制；A 表示攻击者；$D^{i,0}\space and\space D^{i,1}$ 表示两个邻接数据库；b表示实验下标。则最终的输出结果可以用V^{b}来表示：

        $R^{b}$可以代表攻击者A随机扔出的一个骰子，结果为0或者1，代表两个实验。其余的Y_{1-k}表示的是k次查询的结果。

        这个输出是一个多维的随机变量，有着对应的分布。我们的目标是让基于任意两个邻近数据集得到的两个输出之后，对应的分布差异应该尽可能小，以至于攻击者不知道采用了哪个数据集。两个分布的差异就是Privacy loss。如果严格约束，那就是ε-差分隐私；如果允许一定程度违背，那就是(ε，δ)-差分隐私。

        定义：$c_M(o,D,D')\triangleq ln\frac{Pr[M(D)=o]}{Pr[M(D')=o]}$为“两个相邻数据集D和D’，输出o，随机函数M，该随机函数造成的隐私损失”。

        这样我们就有(ε，δ)-差分隐私的充分条件了：隐私损失函数c_M满足：$Pr[c_M(o,D,D')>\epsilon]\leq\delta$

        即，隐私损失大于ε的概率小于δ。

• 串行组合：同一数据集，不同查询函数。一个查询函数 M_i 满足 {ε_i}-差分隐私算法，那么所有的算法作用于同一个数据集 X ，这些算法构成的集合 M_i(X) 满足 {Σ_i ε_i}-差分隐私。

• 并行组合：不同数据集，不同查询函数。一个查询函数 M_i 满足 {ε_i}-差分隐私算法，D_i 表示互不相交的数据集，M_i(X ∩ D_i)表示各个差分隐私算法之间作用的数据集互不相交，那么整体满足 ε-差分隐私。一个推广是，如果 M_i 满足 ε_i 的差分隐私算法，那么整体满足 max{ε_i}-差分隐私。

        这里引入两个相关的引理，详细的论证过程可以参考这里。

（1）（期望的上界）如果k个随机函数(M1, M2, … , Mk)均满足(ε，δ)-差分隐私，那么：

（2）（吾妻不等式，Azuma’s Inequality）假设存在k个随机变量C1, C2,…, Ck，满足对于任意i∈[k]都有$|C_i|＜a$， 且$E[C_i|C_1=c_1,...,C_{i-1}=c_{i-1}]\leq \beta$ ，那么有：

        至此，我们掌握了：

• 隐私损失值的上界：由dp的定义给出$Pr[c_M(o,D,D')>\epsilon]\leq\delta$

• 隐私损失期望值的上界：由引理1给出：$E[c_{M_i}(o,D,D')|M_{1:i-1}]\leq\epsilon(e^{\epsilon}-1)$

• 组合的概率上界：$Pr[Σ_{i=1}^kC_i＞k\beta+za\sqrt k]\leq e^{-\frac{z^2}{2}}$

        根据吾妻不等式，我们就可以得到了强组合定理：

• 强组合定理：

        $\forall \epsilon,\delta,\delta'\geq0, \space if\space M_i\space is\space random-function\space with \space (\epsilon,\delta)-DP, then:$

        可以发现，总的ε不再像基本组成里一样随着k线性增长，而是随着 $\sqrt{k}$ 线性增长。（ε较小时，后面那项近似于0）

        最后便是第一篇论文《Deep Learning with Differential Privacy》中提到的矩统计(Moments Accountant)。

        在基本组合定理里面，考察的是“隐私损失值”的范围。

        在强组合定理里面，考察的是”隐私损失值的期望”的范围。

        而“期望”又被称为“一阶原点矩”。

        那么，“高阶矩”会不会使得隐私损失函数的上界更小呢？

        Adadi等人于是提出了“矩统计”算法。他们使用了SGD算法，针对高斯分布的特例，使用了二项展开，证明了矩生成函数的上界可以像隐私损失一样累加。

        假定SGD的随机选择概率为q，训练轮数为T，则这一系列T个高斯机制 M_i 所构成的组合满足$(q\epsilon\sqrt{T},\delta)-DP$。

2.2.3 超参数#

        超参数就是在开始机器学习之前，就人为设置好的参数。区别于通过训练得到的模型参数，通常情况下需要对超参数进行优化，给学习机选择一组最优的超参数，以提高学习的性能和效果。

2.2.4 随机梯度下降算法SGD#

        首先我们需要了解“梯度下降法”。

        在大多数的学习任务里面，都不可避免地涉及到某种形式的“优化”。通常情况下，这种“优化”指的是：对于输入参数x而言，最大或者最小化输出函数f(x)。

        这个“需要被最大或者最小化”的函数，我们称之为“目标函数”。当我们把它最小化的时候，我们也可以叫它“代价函数”。

        如果我们想把一个函数最小化，首先想到的肯定是求导数，然后导函数值为0，解出极值点，再根据上升还是下降的趋势来判断极大还是极小值。但是，对于许多高维的函数而言，这样的求解是非常困难的，而且很多时候方程并不可解。因此需要引入“梯度下降”的概念，以此来逼近极值点。

        因为曲面上方向导数的最大值的方向就代表了梯度的方向，所以在做梯度下降的时候，只需要沿着梯度的反方向进行权重的更新，就可以找到全局的最优解。假设损失函数为 $J(\theta)=\frac{1}{2}(h_{\theta}(x)-y)^2,

h(\theta)=\sum_{i=1}^{n}(\theta_ix_i)+\theta_0$ 整个过程可以如下描述：

        梯度下降算法一般包括“批量梯度下降”、“随机梯度下降”、“mini-batch梯度下降”三种情况，主要的区别在于每次更新时使用的样本量。

• 批量梯度下降：每次更新时使用所有的样本，对θ的调整，所有样本都有贡献。对于最优问题、凸问题，也可以达到一个全局最优。但理论上一次更新的幅度是很大的，样本越多，更新一次的时间就越久。

• 随机梯度下降：每次更新时使用1个样本，该样本随机采样于数据集。由于该算法的特性，随机梯度下降计算得到的并不是一个准确的梯度，最终收敛时很有可能不是全局最优解。但收敛速度更快，很多时候结果也可以接受。

• mini-batch梯度下降：每次更新时使用b个样本。这是一种折中的方法，但注意采样的方式，可能会收敛到局部最优解里去。

2.2.5 生成对抗网络GAN#

        GAN主要用于图像方面的工作，其思想是：假设有两个网络——Generator和Discriminator。它们的功能是：

• Generator，是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声来生成图片，记作G(z)。

• Discriminator是一个判别网络，用于判别一张图片是不是“真实的”。它的输入参数是x，x代表一张图片，输出D(x)代表x为真实图片的概率。如果为1，则为100%真实的图片，0表示不可能为真实的图片。

        在训练的过程中，生成网络G的目标就是尽量生成真实的图片去欺骗判别网络D，而D的目标就是尽量把G生成的图片和真实的图片分别开来。两者陷入了一个动态的博弈过程。

        在理想的情况下，G可以生成足以乱真的照片，而D难以判定是不是真实的。也即，D(G(z))➡0.5。

        使用数学语言来描述，如下所示：

• x表示真实的图片，z输入网络G的噪声，G(z)表示G网络生成的图片

• D(x)表示D网络判别真实图片是否真实的概率，D(G(z))表示D网络判别G网络生成图片是否真实的概率。

• G希望生成的图片越逼近真实值，也就是D(G(z))越大越好，这样上式V(D,G)就越小，因此G代表了min的趋势。

• D希望判别的越准确，也即D(G(z))越小，因此D代表了上式max的趋势。

        使用随机梯度下降法来训练G和D，过程如图所示：

        根据训练的目标，每次训练D时，D希望V(D,G)越大越好，因此加上梯度；而训练G时，希望V(D,G)越小越好，因此需要减去梯度。整个过程交替进行。

2.2.6 凸问题#

        这是在“梯度下降”里才会遇到的问题。

        梯度下降算法往往是在寻找一个“优化”的解，但由于选取梯度的问题，有可能会收敛到一个局部最优解上去。

        而凸函数则有一个特别的性质：局部最优点就是全局最优点。

        如果可以提前判明优化函数的凹凸性的化，将会对后续的训练过程带来不少的帮助。

        同时，寻找一种普适的梯度下降算法也成为了热门的话题。

2.2.7 范数(norm)、矩(moment)#

        这里仅作简单介绍：

范数：

• 1-范数：$||x||1=\sum{i=1}^n|x_i|$

• α-范数：$||x||{\alpha}=(\sum{i=1}^n|x_i|^{\alpha})^{\frac{1}{\alpha}}$

• ∞-范数：$||x||_∞=\underset{1\leq i\leq n}{max} |x_i|$

矩：

        对于连续变量x和其单变量概率密度函数p(x)，其n阶矩被定义为：

如果是离散型变量，P(x)为x的概率，那么为：

三、解释疑问#

3.1 差分隐私引入深度学习，究竟是为了获得什么？#

        我之前一直以为是**“差分隐私”机制里面引入了“深度学习”的概念**，于是就产生了这个疑问：差分隐私引入深度学习，究竟想要学习什么东西呢？(ε，δ)参数吗？但是三篇论文中间也没有相关的部分啊？

        现在来看，问题应该反过来，应该是**“深度学习”中引入了“差分隐私”机制**，使得训练过程遵循差分隐私的规范，从而起到隐私保护的作用。

        要理解这一点，首先应该从差分隐私的背景出发。也即，2006年的网飞悬赏事件。以下事件引用自维基百科：

2006年10月，网飞提出一笔100万美元的奖金，以奖励可将其推荐系统改进10%的参与者。为此，网飞发布了一个训练数据集供开发者训练其系统。在发布此数据集时，网飞提供了免责声明：为保护客户的隐私，可用于识别单个客户的所有个人信息已被删除，并且所有客户ID已用随机生产的ID替代。

然而，网飞不是网络上唯一涉及电影评级的网站。其他很多网站，包括IMDb，亦提供类似的功能：用户可以在IMDb上注册和评价电影，且也可以选择匿名自己的详细资料。德克萨斯州大学奥斯汀分校的研究员阿尔文德·纳拉亚南和维塔利·什马蒂科夫（Vitaly Shmatikov）将网飞匿名化后的训练数据库与IMDb数据库（根据用户评价日期）相连，能够重新识别网飞数据库中的个人。这表明网飞采取的匿名化手段仍然可以泄露部分用户的身份信息。

        这说明匿名化的方式并不能保证用户隐私。

        德州的研究员们所采用的方法，也就是“根据数据集”差异性+“发布时间”的逻辑推导，这构成了后续一系列隐私攻击的基础。所谓“差分隐私”，“差分”，就是数据集之间的差异。

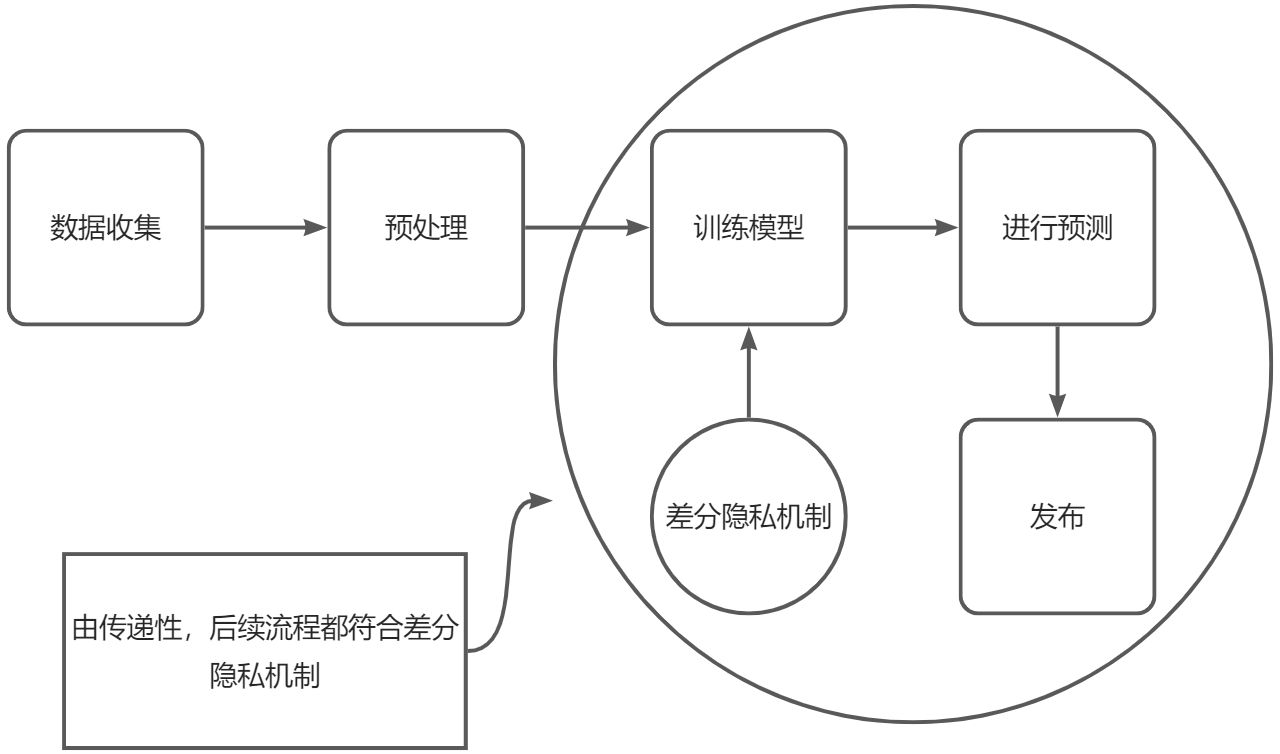
        回到深度学习系统上来。它的基本框架是由以下四步组成的：

• 构建深度模型，初始化模型参数

• 输入训练数据，并计算梯度

• 用梯度下降法更新模型直到收敛

• 将收敛的模型用于数据预测

        这四步，涉及到了**“训练前”的原始数据**、“训练中”的过程，“训练后”的模型参数。

        在一般的训练中，训练数据很有可能私下签到协议才能正规采集的，对外界而言，是隐私数据，不能泄露。所以需要对模型进行隐私保护。

        最常规的想法，是直接对预测添加噪声。但是，深度学习的模型参数是很容易获取的，所以仅仅在预测阶段添加噪声，往往无法达到隐私保护的目的。就像网飞往预测模型里面抹去了用户信息，攻击者仍旧能够获得隐私数据一样。我们仍旧要回归到深度学习的过程上来。

        根据差分隐私的传递性特征，对于满足(ε，δ)-差分隐私的随机算法M，对它的结果进行任何形式的处理，所构成的新算法f·M，同样满足(ε，δ)-差分隐私。因此，对深度学习模型添加差分隐私的环节应该尽可能靠前，使得差分隐私机制覆盖尽可能多的流程。

        直接在“训练前”的原始数据里面添加噪声可以吗？

        答案很显然——不行。直接往训练集里添加噪声，会使得数据集本身变脏，难以使用，因为往往需要添加大量的噪声。

        那在模型参数里面添加差分隐私机制呢？

        深度神经网络是一个对参数非常敏感的黑箱，直接对训练好的参数添加高斯噪声会直接使得整个算法完全失效。

        综上，深度学习里面添加噪声，只能够是在“训练过程”中，通过在训练过程中对梯度进行裁剪并添加高斯噪声，可以保证训练过程的差分隐私性质，再根据传递性的特点，该特性可以传达到后续的推断过程中。

        整个过程如图所示：

3.2 拓展——Renyi Differential Privacy(RDP)#

        我在查询矩统计的相关文献时，看到过一些帖子上有关于“RDP”的介绍，这种方法能够划定出比矩统计更加紧的上界，且计算效率更高。于是在此简单介绍一下。本节主要内容主要来自此篇文章（RDP）以及这篇文章（瑞丽熵）。

        首先是瑞丽熵的介绍，这里直接给出定义公式：

        我们可以把它写成“α-范数”的形式：

        不难发现，当α➡1时，利用0/0型洛必达法则，可以把瑞丽熵化为香农熵：

        而当α➡∞时，我们得到的就是最小熵：

        这里用到了无穷范数的证明，暂且略过。

        讲完瑞丽熵的定义了，我们再来回顾一下“差分隐私定义”的推导过程是怎么样的。可以根据之前写的这篇博客简单了解一下。

        简单来说，我们是使用“相对熵”的概念来比较两个数据集之间的差异的。

        而根据瑞丽熵的定义，我们不难发现，瑞丽熵其实就是相对熵的推广。如果我们把推导时的**“相对熵”替换为“瑞丽熵”的话，是否能够得到更一般的差分隐私定义**呢？

这里直接给出瑞丽分歧(Renyi Divergence)：

        当α➡1时，同样是0/0型的洛必达，同上面推导，此时瑞丽分歧将会转化为KL-分歧：

        这正是我们推导差分隐私定义时所用的。

        而如果把“KL-分歧”替换为“瑞丽分歧”，那么差分隐私的定义就会被修改为：

        其中，M(d)(θ)表示在训练集d上训练所得结果为θ的概率密度，也就是 $M(d)(\theta)=Pr[M(d)=\theta]$ ,α∈(1,∞)。我们称上面这样的M满足(α，ε)-RDP。对照一下差分隐私的定义，我们不难发现，如果机制M满足(α，ε)-RDP，那它也一定满足$(\epsilon+\frac{log(1/\delta)}{\alpha-1},δ)-DP$（直接把参数代入到定义中，移项即可）。

        根据RDP的这篇文章的推导，我们可以得到一个比矩统计还要紧的上界。这里直接给出结论：

• 对于任意的 α≥0，在 t 时刻具有随机性的训练机制Mt满足：

        那么整个训练系统M则至少具有：

        或者替换成常规差分隐私的表达形式：

• 对于任意的 α≥0，在 t 时刻具有随机性的训练机制Mt满足：

        给定δ，则最佳的ε取值为：

        给定ε，则最佳的δ取值为：

        RDP给出了一个比Moment Accountant更紧的上界。