一、任务说明
总结这两周学习的三篇论文的知识内容
整理论文中出现过的知识、方法、定理
对一些必要的知识点进行拓展学习
二、知识词典
2.1 主要内容概括
3-4-Differentially Private Distributed Data Analysis
| 属性 | 描述 |
|---|---|
| 作者 | Hassan Takabi … |
| 场景 | 用户的数据如果是从多个来源收集或者多个实体之间互相共享的话,那么用户隐私将会产生很大的问题。 |
| 问题 | ①大多支持集中式的数据库,而非分布式的数据库; ②在分布式数据集中容易产生“串通”; ③需要在隐私和效率之间进行权衡; ④在交流和计算成本上效率低下…… |
| 方案 | DstrDP:随机选择算法+同态加密+差分隐私。 |
| 创新 | • 随机选择算法,由算法随机指定一人(且只有他自己知道)添加噪声,避免了全部添加噪声造成的巨大隐私成本和精确度下降 • 采用同态加密,安全性相比secure sum更高,即使发生了串联,对方也不知道数据内容。 • 本质是介于secure sum和SuLQ之间,既不是直接公开,也不是全部添加噪声,而是随机选择一人添加噪声,再对集成结果添加噪声。并且把SDQ的secure sum换成了HE。 |
| 不足 | • 对于“恶意攻击者”的威胁模型缺少探讨,只能针对“半诚实”的威胁模型。所有的前提都基于集成者不泄露私钥的前提下。 • 组合定理过于宽泛,基于的是最基本的组合定理。如果能够使用强组合、矩统计或者RDP组合定理,精确度还能进一步提高 • 在构建决策树时,基本上只有自己结果的对比,缺少和其他方案成果的对比 |
3-5-A New Differentially Private Data Aggregation With Fault Tolerance for Smart Grid Communications
| 属性 | 描述 |
|---|---|
| 作者 | Haiyong Bao, Rongxing Lu |
| 场景 | 在智能电网系统中,用户家中所有的数据都会连接到一个中心元件——智能电表里面,它会定期收集电器的耗电量并将其报告给本地网关GW,网关将数据集成再转发给CC做进一步的分析和处理,比如做出实时电力定价决策、检测电力欺诈或者泄露。 但是,实时地使用数据,这里面会包含不少用户的用电模型,与用户的隐私高度相关,因此需要对其进行隐私保护。 |
| 问题 | ①同态加密技术对于“honest but curious”下的CC并不保险; ②不具备容错率,智能电表作为一种廉价的商品,稳定性并不可靠; ③难以抵挡差分攻击。 |
| 方案 | CC 包含三个私钥 Y_i, s_0, r,U_i 包含一个私钥 s_i,GW 包含一个私钥 t 通过设计一套同态加密以及优化方法,使得在整个过程中,数据式子里面都至少包含两个的私钥,这样确保了数据的安全性。 s_0私钥管理的算法,确保了在存在部分电表损坏的情况下,仍旧能够执行流程,且整个过程不依赖内存存储,具备很高的容错度。 |
| 创新 | • 差分隐私部分利用了拉普拉斯无限可分机制,这样使得每个用户单独添加噪声再集成后,不至于整体的隐私成本过大,损害数据可用性 • 利用加密密文的方式实现了容错度,不依赖于额外的缓存消耗,对空间的要求更低 • 由TA分配了初始化私钥,在从用户端上传的流中,中间数据始终保持了两个私钥,攻击者即使掌握了某一方的数据,也无法通过暴力破解隐私数据 • 网关只负责转发和基本的运算工作,核心压力较小。这样设计的成本会更低 • 在添加删除用户时,只需要重新分配私钥即可,操作简单 |
| 不足 | • 涉及了较多的幂运算、积分运算,在用户数量较多的时候,时间复杂度可能会高一些,属于时间换空间• 文中使用的Boneh-Goh-Nissim加密方式是一个有限次全同态加密手段,仅支持1次乘法同态计算。放到现在来看,有了更多的全同态加密手段,应该可以使得保密等级更强。 |
3-7-PrivSyn Differentially Private Data Synthesis
| 属性 | 描述 |
|---|---|
| 作者 | Zhikun Zhang … |
| 场景 | 差分隐私里一个颇具挑战的问题是:如何生成一个能够在隐私数据里高效捕获有用信息的合成数据集?这个数据集能够在对现有算法不进行任何隐私关照和改动的前提下,允许完成所有的任务。 |
| 问题 | PrivByes和PGM方法存在诸多问题: • 作为一个旨在提供关于联合概率分布的一种紧凑表示的图模型,它在设计上是稀疏的 • PrivByes 技术采用了交互信息来选择边际,但交互信息的敏感度是很高的 • PrivByes 的改进算法,计算复杂度很高 • PGM 算法缺少自动选择机制 |
| 方案 | 1. 首先是过滤和合并,把边际里计数低于阈值的合并起来,如果值仍旧低于阈值,那么直接舍弃;否则合并成一个新的边际来代表这些边际。 2. 其次是在差分隐私标准下选择边际。作者在这里抛弃了高维的边际,而是采用了2维边际。作者提出了度量标准:InDif,用来评估 实际2维边际 和 假设2维边际 之间的距离。 3. 然后是进行后处理,这一步主要处理一致性的问题,包括“引入噪声导致概率和不为1或者概率为负”以及“部分属性重叠计算导致的不一致性”。 4. 在后处理完毕之后,便开始进行最后的数据集生成,这里采用了逐渐更新方法GUM。 |
| 创新 | • 提出了一种“关联性度量”的标准,即 InDif; • 提出了一种贪心算法,来自动过滤、捕捉、选择、合成符合要求的边际; • 全文两处进行了权衡:最小化误差(噪声误差和依赖性误差的权衡);一致性权衡(属性重叠、引入噪声导致的概率和不为1或概率为负) • 基于以上3点,作者的方法在敏感度下要胜过采用了交互信息的贝叶斯法,在操作上要胜过手动的马尔可夫随机场。同时由于使用的是贪心算法,算法复杂度要远低于以上两者。 • 有针对低计数、单维度的边际的处理(过滤和合并、不一起处理而是在最后再添加单维度的边际)。 |
| 不足 | • InDif 目前还只能处理表格形式的数据,对于图像问题还需要进一步的研究以及映射。 • 为了避免计算复杂度的过高,作者抛弃了一些高维度的边际。这使得算法本身会损失了一些高维度的相关性。 |
2.2 知识点整理
2.2.1 l1 和 l2 误差
在上次总结里,我们介绍过 α范式 :

而如果把上式的 x_i 替换为 x_i-y_i,那么 α范式 就能变成机器学习里常见的 闵可夫斯基距离了:

特别的,当 p=2 时,闵可夫斯基距离就将变为欧氏距离。p=1 时,将变为曼哈顿距离:

某种意义上来讲,曼哈顿距离就可以当作是“L1”误差来理解。
机器学习中常说的 L1 L2误差,其实就是两种不同的损失函数。他们的形式是这样的:

其中,f(xi)为估计值,y_i为目标值。L1 L2误差的根本目的是反应目标与估计(或者说,期望)之间的距离,并希望通过调整参数,来把这个距离最小化。L1损失函数可以称为 “最小绝对值距离”(LAD),或者 “绝对值损失函数”(LAE)。L2损失函数可以称为 “最小平方误差”(LSE) 。
由于采用了不同的计算方式,因此体现的效果也不一样:
L1损失函数相比于L2损失函数的鲁棒性更好。因为L2采用的是“平方”,如果误差数值超过1,那么误差会放大很多倍,模型对数据会异常敏感,这样会牺牲很多数据。
如果是图像重建任务,如超分辨率、深度估计、视频插帧等,L2会更加有效,这是由任务特性决定了,图像重建任务中通常预测值和真实值之间的差异不大,因此需要用L2损失来放大差异,进而指导模型的优化。
L1的问题在于它的梯度在极值点会发生跃变,并且很小的差异也会带来很大的梯度,不利于学习,因此在使用时通常会设定学习率衰减策略。而L2作为损失函数的时候本身由于其函数的特性,自身就会对梯度进行缩放,因此有的任务在使用L2时甚至不会调整学习率,不过随着现在的行业认知,学习率衰减策略在很多场景中依然是获得更优模型的手段。
在机器学习的过程中,通过对损失函数不断求导以此使得估计函数与目标值不断趋近。但这样也会存在“过拟合”的问题。为了解决这个问题,就必须引入“正则化”的思想。L1正则和L2正则的函数如下所示:

要理解“正则化”的作用,我们需要对L1和L2分别进行偏导。假设超参数λ已知,η为步进,sign(w_i)是符号函数,那么对于L1,有:

这个思想和积分差不多,算出损失函数在wi时的偏导,然后按照这个方向前进η步,不断循环。梯度下降SGD就是这样学习的。同理,对于L2,有:

对于L1,由于是“绝对值”的形式,因此在 wi=0 处不可导。此时,如果在 wi=0 左右的导数方向相反,那么 wi=0 必然是一个极值点。因此,L1迭代往往会把参数迭代成0,导致“稀疏性”。我们可以利用这一性质来进行特征提取。
对于L2,首先不存在上述问题。其次,我们发现,如果wi越大,那么每次下降时的数值也会很大,这样就会使得最终迭代的参数系数并不会太大,这就避免了因为“拟合系数过大,导致过拟合问题”的发生了。
2.2.2 Marginal 边际
在浙大的那篇论文里,出现了不少“Marginal”。一开始我很难理解,甚至给自己胡乱解释了一下(物联网里面有过边缘计算的概念,一开始就往这个方向联想了)。直到看到wiki里的解释:
These concepts are “marginal” because they can be found by summing values in a table along rows or columns, and writing the sum in the margins of the table
原来就是在联合概率表里面,“不考虑另一事件的结果,只关注其中一个事件的概率”,这些概率通常写在表格的边上,所以就叫“边际”marginal了…
如图所示:
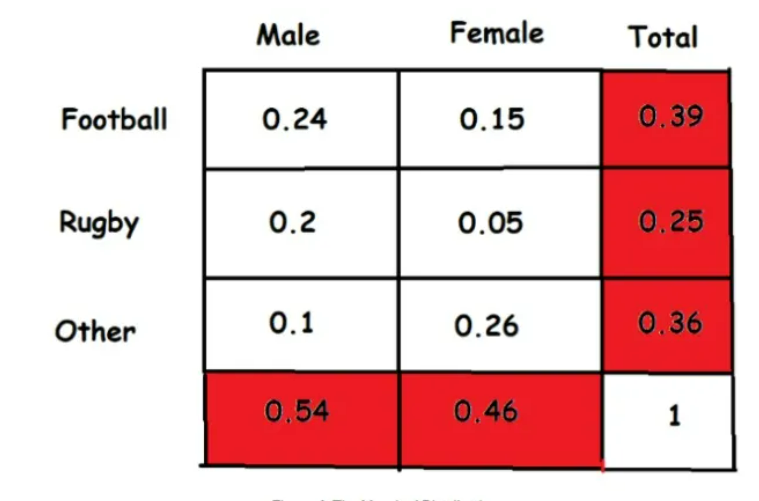
这里面,Marginal 就是标红的部分,与条件概率相对。
2.2.3 z-CDP相关知识
中心思想就是把 (ε,δ)-DP 和 renyi分歧 连接起来,这样就能够有效使用 renyi分歧的性质来获得更紧的组合特性。
【定义】:一个随机机制是A 是 p-zero集中差分隐私 ,当且仅当对于任意两个邻近数据集 D和D’, 以及所有的 α∈(1, ∞),有:

其中,D_α(A(D)||A(D’))是分布A(D)和A(D’)的 α-renyi 分歧。 是概率密度函数的隐私损失随机值。
zCDP具备一些简单的线性组合性质,同时还可以与高斯机制组合:
【定理1】:如果随机机制A1和A2分别满足 p1-zCDP 和 p2-zCDP,那么它们的线性组合 A=(A1, A2)满足 (p1+p2)-zCDP
【定理2】:如果A提供了 p-zCDP,那么对于任意的δ>0,A满足
【定理3】:一个提供了噪声 的高斯机制满足
根据这三条定理,给定 ε 和 δ,我们就能够为每个任务计算噪声的总量。
首先使用定理2,计算满足条件的总共p值。
然后使用定理1,来为每个任务 i 分配一个pi。
最后,使用定理3来为每个任务分别计算 σ。
三、下阶段学习目标
跟着笔记,逐渐学习论文源码
Kaggle上参与1-2个实际的机器学习课题
继续学习联邦学习相关的知识
算法知识不要拉下,每天leetcode打卡学习
