一、任务说明#

        由于最近工程实验较多，算法、质量测试、软件工程…因此这两周研读的进度较小。主要的精力集中于GAN的学习上。在此做简要整理。

• GAN知识框架

• 论文研读

        本科阶段没有接触过很多的机器学习相关的项目，所以难免会有纰漏。主要分享我这几个月来研读相关的一些经验，和自己的推导。

二、知识总结#

2.1 GAN—生成对抗网络#

2.1.1 引言#

        如果最近有关注一些美术、绘画等艺术相关的话题的话，那么“AI作画”肯定是一个绕不顾去的坎。很多热门的AI作画网站，例如：Midjourney、mimic、NovelAI…在最近一到两个月的时间里，频繁占据了各大论坛的热门。画师们从未像现在这样对于新技术有着如此强烈的恐惧感，他们担忧于自己随时可能会被AI取代，但这一切只是技术野蛮生长的时代的开始。在绘画之外，新闻、媒体、娱乐、报道…“AI生成图片”的技术，也在潜移默化地影响着这些行业。8月份四川山火，占据各大头条的这张“逆行者”照片，其实就是AI生成的，而在原作者出来辟谣之前，几乎没有人能够发现。

        AI绘画的飞速发展让人们不得不仔细审视其原理、影响和未来的空间。本次分享我就简单介绍一下AI绘画用到的算法(GAN和diffusion)及其发展历程。本次我们的主题是GAN，所以我会详细介绍GAN相关的原理、算法、以及拓展。对于diffusion的部分，我则做一些简单的介绍和应用。

2.1.2 提纲#

• 生成对抗网络-GAN

• 算法原理

• 简单讲解-DCGAN

• 优化拓展-WGAN

• 扩散算法-diffusion

• 原理

• 优缺点、两者之间的比较

• GAN总结

2.1.3 GAN-原理#

        GAN，全称是：Generative Adversarial Network，即：生成对抗网络。由 lan Goodfellow 于2014年提出。它的原理非常简单，设置两个网络G: Generator 和D: Discriminator，它们分别进行如下工作：

• G：Generator, 生成网络，接收一个随机的噪声z，通过这个噪声来生成图片。我们把它的输出记为 G(z)

• D：Discirminator, 判别网络，接收一张图片 x，判断它是不是“真实”的。它的输出记为D(x)，D(x)∈[0,1]，表示“x是真实”的概率。D(x)=1，表示 x 100%为真实的图片。D(x)=0，表示它不可能是真实的图片。

        在训练过程中，生成网络 G 的目标是尽量生成真实的图片去“欺骗”D，而判别网络 D 的目标就是尽量把 G 生成的图片和真实的图片区分开来。这样一来，整体上就构成了一个动态博弈的过程。由于训练过程没有预先标准，因此 GAN 也是“无监督学习”的一种。

        在理想情况下，G生成的图片足以以假乱真，而 D 难以判定 G 生成的图片是否真实。也就是说：

        更具体一点，我们可以用如下的数学公式来表示GAN的目标函数：

        我们可以这样来理解这道公式：

• D(x) 表示判别器对真实图片输出的概率值，D(G(z))表示判别器对生成图片输出的概率值

• 对于G而言，它希望生成的图片越能以假乱真，因此 G 应该希望 D(G(z))越来越大，最好趋向于1，反应到V(G,D)上，就是V越来越小。因此式子前面写了：$\underset{G}{min}$

• 对于D而言，它希望自己能够精准识别真实图片和生成图片，因此D应该希望D(x)趋向于1，D(G(z))趋向于0，反应到V上，就是V越来越大。因此式子前面写了：$\underset{D}{max}$

        在 Goodfellow 的原论文中，作者给出了GAN算法的如下表现形式：

        其分析如下：

• 两个for循环，外层代表迭代，内层代表训练

• 每次迭代，首先训练判别器D，然后训练生成器G

• 训练过程采用了随机梯度下降算法：

• 对于D：对m张生成图片以及m张真实图片，用D进行判别，取均值然后求其梯度。由于D的期望是使得V尽可能大，因此训练时加上梯度。

• 对于G：对于m张生成图片，用D进行判别，这里只取 log(1-D(G(z)))的部分（因为 x 是真实图片，与G无关）。取均值然后求其梯度。由于G的期望是使得V尽可能小，因此训练的时候需要减去梯度。

        以上就是GAN算法的设计思想。接下来我们用两个实例 DCGAN 和 DPGAN，来给大家讲解一下GAN的实现和应用。

2.1.4 DCGAN#

        我们在这里用DCGAN来完成对于GAN的一个初步了解。它的过程和上面介绍的完全一致，区别在于把上述的两个G和D换成了卷积神经网络，然后卷积神经网络的结构做了一些改变，来提高样本的质量和收敛速度。采用CNN的原因是，CNN是深度学习中对于图像处理应用最好的模型之一。卷积神经网络通过特定的filter，可以识别出图片的某些特征，进而实现图像识别的功能。

        在DCGAN中，生成器的结构是这样的，一共是四层：

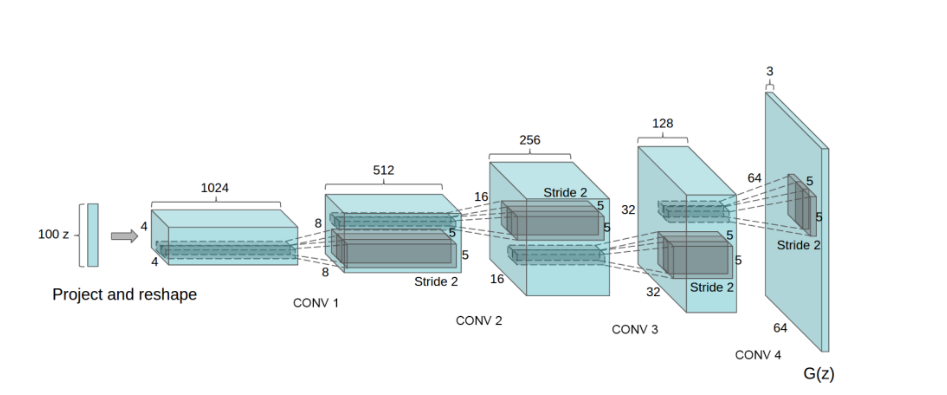
        我们的训练目标比较有趣：我们打算借用DCGAN来生成一系列的动漫风格头像。这个工作首先由日本的一位开发者在2015年圣诞节完成，思路发表在了Qiita上。由于时间的缘故，像现在比较流行的框架tensorflow和pytorch，一个是2015年11月，一个是2017年的，因此这个版本的“头像生成”并没有使用这些现在流行的框架，而是使用了一个比较小众的框架chainer进行训练。

        我们根据其思路，采用tensorflow重写这个程序。代码的重点部分如下所示：

• 首先是生成器和鉴别器，如下所示，完全遵循上述cnn的格式进行模板化的创建：

    - 生成器

    - 判别器

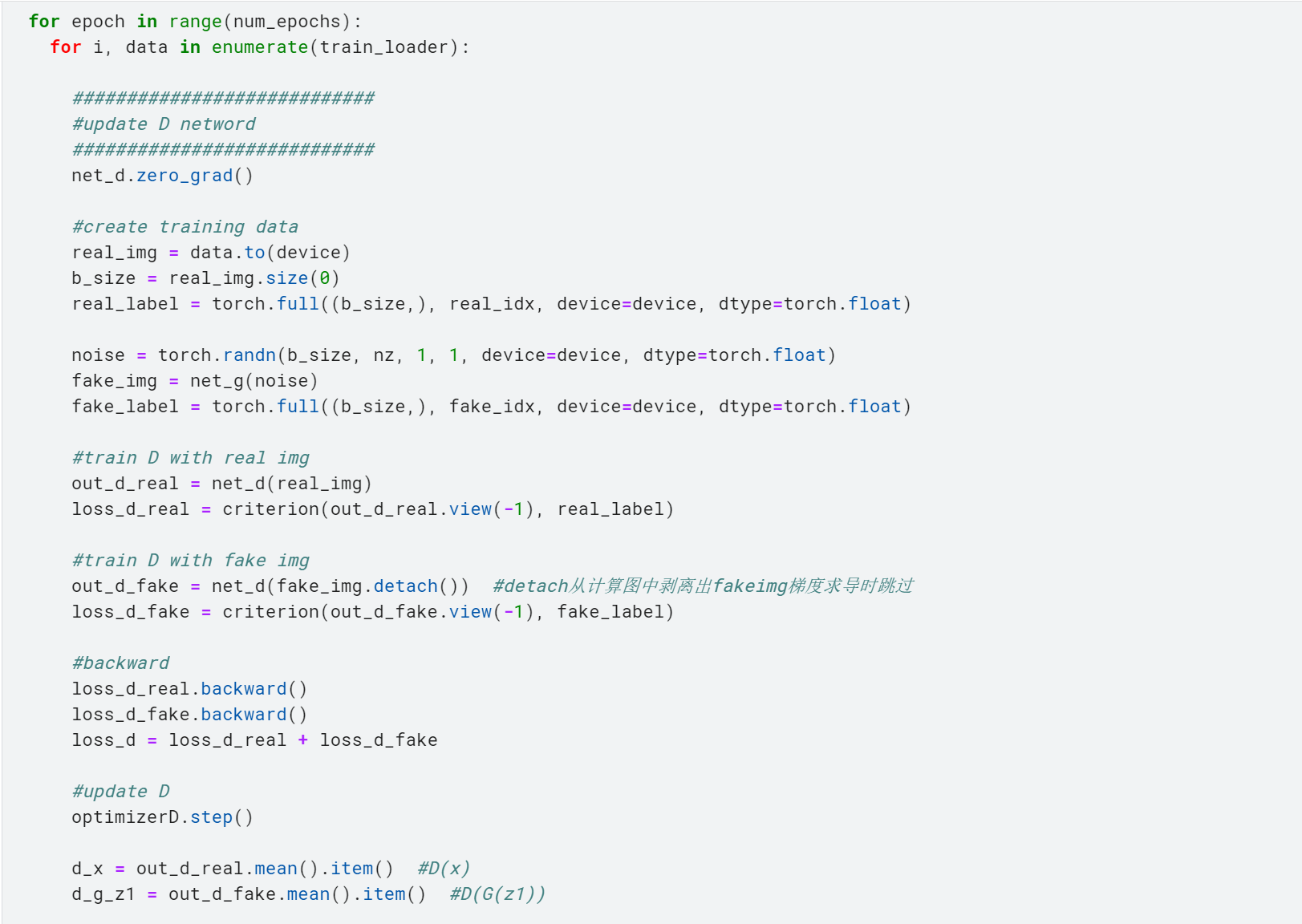
• 训练部分如下所示，我们首先进行的是鉴别器的训练：

    - 1.        在初始化梯度之后，首先使用生成器网络net_g()，传入一个噪声，生成fake_img。

    - 2.        然后使用鉴别器网络net_d()，分别使用真实图片和生成图片让鉴别器去识别。

    - 3.        分别记录下这两者的损失函数。

    - 4.        两者分别通过backward()函数求导，再相加，这就是鉴别器的损失函数了。

    - 5.        通过step()函数来更新参数。

• 然后是对生成器的训练：

    - 1.        在初始化梯度之后，我们使用鉴别器网络net_d()对之前的fake_img进行鉴别

    - 2.        计算生成器的损失函数

    - 3.        通过step()函数来更新参数

    - 4.        训练结果可视化（每50次迭代输出一次中间结果）

    - 需要注意的是，我们计算生成器的损失函数时，不难发现，我们对fake_img计算损失函数时，使用的是real_label，这是一种训练技巧，经验表明对于生成器训练时这样操作，效果会更好一点。

        我们在kaggle平台上进行DCGAN的训练。GPU为Tesla P100，cuda加速，100轮epochs，每轮迭代200次，每一次迭代的 batch_size 为128，一共运行了6.7h。其中，生成器的学习率为0.002，鉴别器的学习率为0.0002。我们制作了一个gif来演示GAN的训练过程：

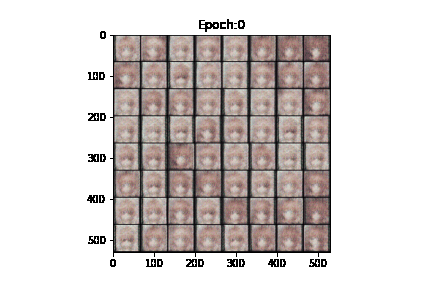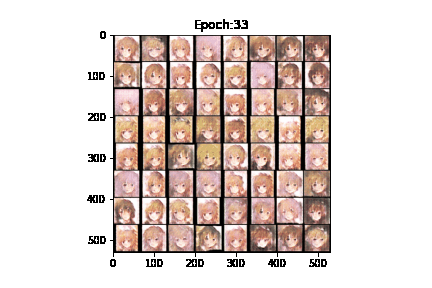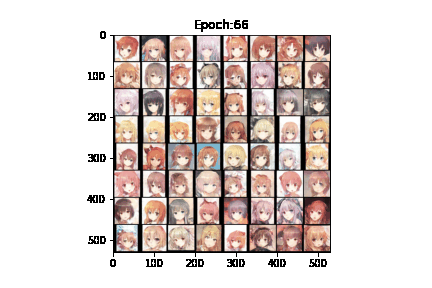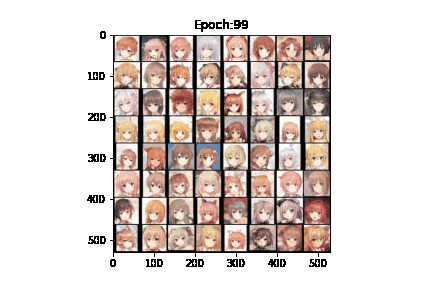
        可以看到，随着训练过程的推进，生成效果逐渐从“噪声”->“模糊的色块”->“大致的人影”->“难辨真假”。

        我们使用了Adam优化，相比起最初版未优化的DCGAN版本，在生成图像的结构、色块…问题上要好了不少：

• DCGAN生成的图像：

• 未优化的DCGAN：

        G和D的损失函数随迭代次数的增加而变化，其图像如下所示。随着迭代次数的增加，对抗逐渐激烈起来，起伏很大。

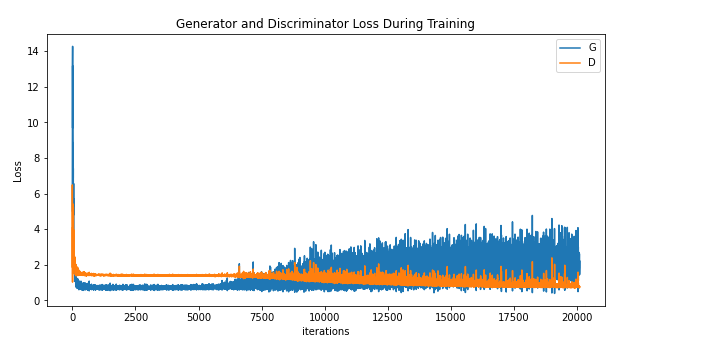
        在编码、训练、调参的过程中，我们也发现了不少问题。这些问题也是GAN的特征，以及它初始算法存在的一些问题：

【问题】：

1、为什么要先训练D，再训练G？

【答】由于刚开始的时候生成器没有反馈，给它一堆随机向量噪声，他生成图片的质量一开始必然是低下的，那么鉴别器很容易就能识别并且判假。

如果先训练生成器，再训练鉴别器，生成器G依靠上一轮的鉴别器D结果来更新，而鉴别器D直接对着这一轮的生成器G结果进行判别，整体上就会呈现鉴别器的优势。如果鉴别器的训练太强了，就会产生梯度消失的问题。这种训练对鉴别器是有益的。

        交换一下训练顺序，先训练鉴别器，鉴别器D依靠上一轮生成器G的结果进行判别，生成器G根据这一轮的鉴别器D结果来更新，整体上会更有利于生成器的训练。

         而在训练GAN的时候，我们往往会要求鉴别器D的训练不要太强。因为GAN的本质目的还是“生成”，“判别”只是有一个辅助的作用。判别器D的训练太好了，后期容易造成生成器的梯度消失。

2、为什么训练生成器时，我们明明是对D(G(z))求梯度，但label仍旧是“real_label”？

【答】这是一种训练技巧。

        首先我们从“最终结果”入手来考虑其合理性。理想情况下，鉴别器D应该判别不出生成器G结果的真假，也就是这个时候，real_label还是fake_label，在鉴别器眼中是无意义的、等价的。因此，从最终结果入手，把fake_label设置成real_label并不影响理想情况的合理性。

        这样训练的一个好处是，对于一个fake_img，如果一开始效果很差，那么鉴别器很容易就判定为假，此时标注却为真，整体误差会很大。大误差通过backward()求导反向传播，会造成生成器网络的大更新。

        反过来，如果这是一个fake_img，但生成器的效果很好，那么鉴别器就容易判定为真，此时标注也为真，那么误差就会很小，小误差反向传播，只会对生成器网络的参数进行微调。

        这样就使得生成器网络的更新符合生成效果的迭代了。

3、如何理解损失函数？

【答】这需要和损失函数的计算方式联系起来。

        我们首先需要明白一点：判别器是如何确定一张图是真是假的？——当然是比较这张图和真图的“相似性”。这么说可能比较模糊，我们用更严格的表示：

• 对于一张图，我们可以把它映射到一个三维矩阵上：使用“像素点的位置+RGB通道”来描述。这样，就可以把图片转化成一个分布。

• 鉴别器比较图片和“真图”的相似性，就是比较这两张图分布的相似性。

• 图像的相似性问题——>分布的相似性问题——>比较信息熵。

        衡量分布的相似性问题，我们可以使用“相对熵”的概念。给定两个分布p(x)和q(x)，p(x)相对q(x)的相对熵被定义为：

        从公式上理解，相对熵其实就是交叉熵和香农熵的差。这道公式在后面的WGAN里会用到，这里就暂时做一个简单的介绍。

        很显然，如果p(x)和q(x)越接近，那么相对熵就会趋向于0。因此，如果使用相对熵来衡量分布的差距，那么训练的目标应该是使得相对熵不断地逼近0。

        我们可以通过吉布斯不等式来证明，相对熵具有非负性。同时由其公式本身可以看出，相对熵具备非对称性。这使得相对熵在计算一些非对称的分布差距时具有良好的表现，比如“差分隐私”。但是，在GAN中，这种特性就很致命了。比如，A和B的距离为t，那么B和A的距离自然也应该为t。但是，由于相对熵的非对称性，这就使得：

        因此，我们需要对相对熵进行一些简单的改变，使得其具备对称性。一个很朴素的想法：

        这样就使得分布具备了对称性。这就是JS散度，也是GAN初步时普遍采用的损失函数计算方式。

        不同的损失函数直接影响了参数更新的方式，从而影响了GAN的性能，因此对于损失函数的选择也是有效训练GAN的难点。

        以上便是GAN算法最基本的框架和梗概。下面主要介绍一下GAN的主流拓展——WGAN。它主要用于解决JS散度的梯度消失问题。

2.1.5 优化拓展——WGAN#

        仔细观察JS散度，我们把m的表达式代入其中：

        由于GAN的训练，本质是通过更新参数，来把G生成图像的分布不断逼近真实的图像分布，在这个过程中，会存在一个很尴尬的问题，如下所示：

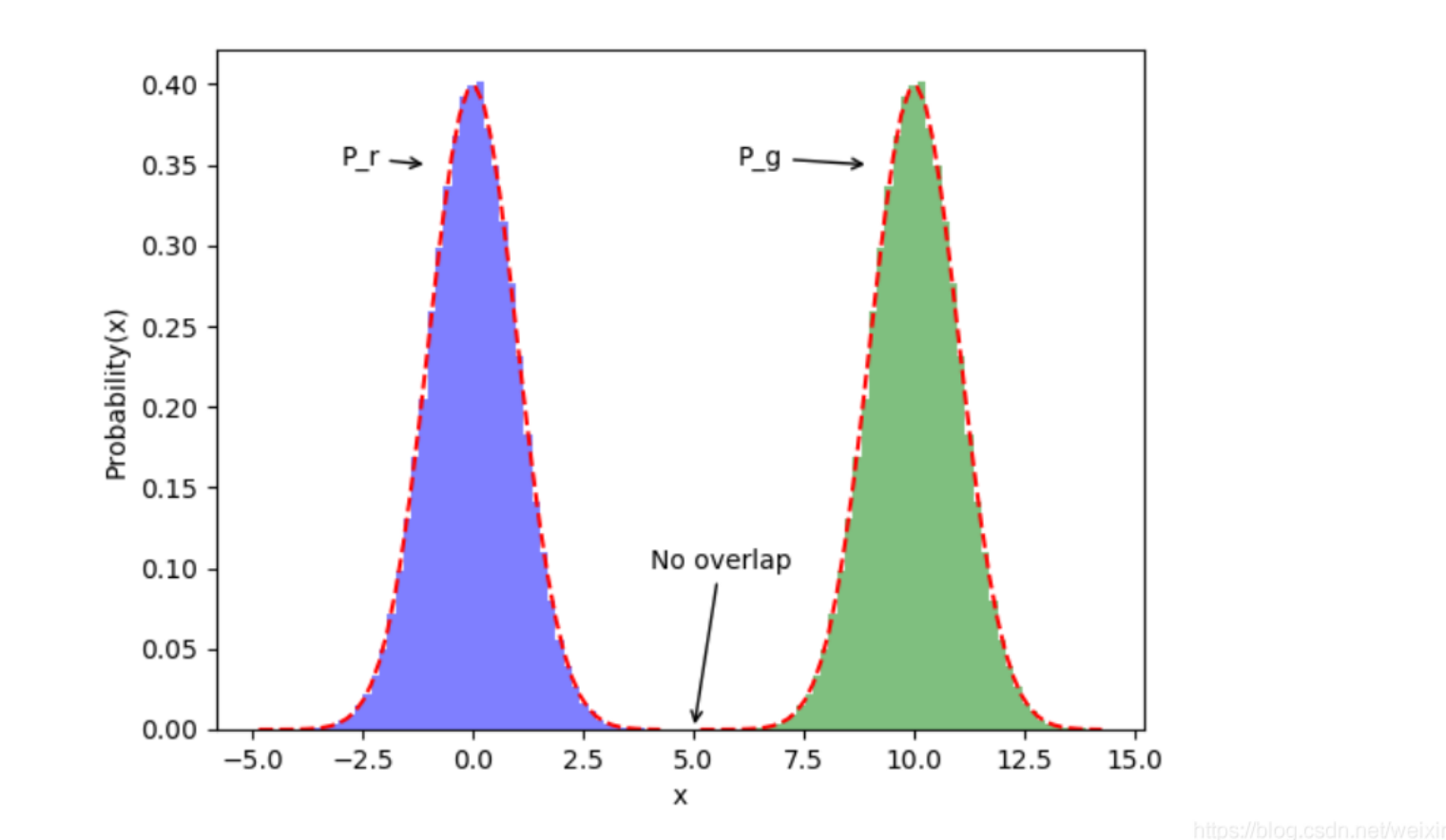
        两个完全不重叠的正态分布在不断靠近的过程中，肯定是从p(x)（或q(x)）趋向于0的部分开始逐渐重叠、靠拢的。但当我们把p(x)=0或者q(x)=0代入JS散度的公式时，我们会发现，JS值会恒等于 ln2。证明如下：

• 假设存在完全不重叠的点x0，当x>x0时，有p(x)趋向于0，当x<=x0时，有q(x)趋向于0。则对于x>x0时：

• 同理，当x<=x0时，q(x)趋向于0，同上论述。

        我们这就发现了JS散度的致命缺陷：如果一开始两个分布完全没有重叠，那么不管两个分布的中心有多近，JS散度值恒定为ln2，无法通过梯度下降算法来求解。梯度消失了。

        为了解决这个问题，2017年的时候，Martin Arjovsky等人发表了著名的《Wasserstein GAN》论文，提出了一种全新的度量方式Wasserstein距离，它是这么定义的：

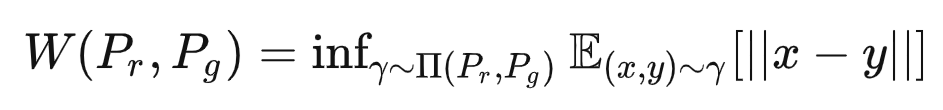
        其中，$\Pi (P_r, P_g)$表示 Pr 和 Pg 组合起来的所有可能的联合分布的集合。对于其中每一个可能的联合分布γ，我们可以从中采样出一个 (x,y)，其中 x 为真实样本，y 为生成样本，然后计算这两个样本的距离 || x - y ||。接着对这个距离求期望 E。 这样，每一个可能的联合分布就对应一个可能的距离期望。在所有期望中选取下界 inf，我们把这个下界定义为 Wasserstrin 距离。

        我们可以这样形象地去理解这个 Wasserstein 距离：把两个分布想象成两个沙土堆，现在我们需要计算两个沙土堆之间的差距，而Wasserstein 距离就相当于一个推土机，它不断地从把Pr这堆沙土挪到Pg位置（求||x-y||），并且计算中间的消耗(求期望)。而W(Pr, Pg)就是所有消耗中最小的（求下界inf）。因此，Wasserstein距离又被称为“推土机距离”。

        Wasserstein距离相比KL散度、JS散度的优势在于，首先它具备对称性（||x-y||），其次它在两个分布完全不重叠的时候，并不会产生JS散度那样梯度消失从而无法指引学习的困境。

        在原论文中，作者采用 Wasserstein 距离作为判别的标准，并且改进了GAN的训练过程，提出了WGAN算法：

        相比起 lan Goodfellow 的初始版本，WGAN一共做出了以下四点改变：

• 去掉判别器最后一层的sigmoid

• 判别器的f采用wasserstein距离，损失函数loss不取log

• 每次更新判别器的参数之后，把它们的绝对值截断到不超过一个固定常数c

• 不要用基于动量的优化算法（包括momentum和Adam），而是推荐使用诸如RMSProp等的优化函数。

        比较有意思的一点是，上述的第三点采用了一个clip函数，它的作用是把判别器的更新幅度上限限制到C，从而避免了判别器的更新幅度过大、性能太强，导致生成器的“积极性”遭受过大打击。这种采用 clip 的思想算是一个比较常用的技巧，在2016年差分隐私领域的经典论文《Deep Learning with Differential Privacy(CCS)》中就采用了这种方式来进行SGD训练。而lan Goodfellow对那篇论文也有不少的贡献。

2.1.6 Diffusion算法#

        最后，我们再简要介绍一下图像生成领域的新星——Diffusion算法。在之前，利用GAN生成图像虽然引起了相关领域工作者的一些兴趣，但大部分画师还是将其视作“玩具”，AI绘画虽已造成了冲击，但还不是这么强烈，主要受影响的是那些只会画“大头画”的入门级画师。直到2020年扩散算法的提出，以及2022年stable-diffusion的开源，这种冲击终于变成了绘画大厦上的乌云，犹如20世纪初彻底摧毁了物理学大厦上的乌云一样。

        Diffusion 正式提出是在2020年的一篇名为《Denoising Diffusion Probabilistic Models》（简写为DDPM）的论文，在该论文中，作者论述了Diffusion算法的基本思想，它主要包括两个方面：

• 前向过程：往一张图片里面不断添加噪声，直至整张图片都变白为止。

• 逆向过程：基于马尔可夫链，逆向学习上述的加噪过程，也即学习：“一张满是噪声的图是如何变成一张图像的”

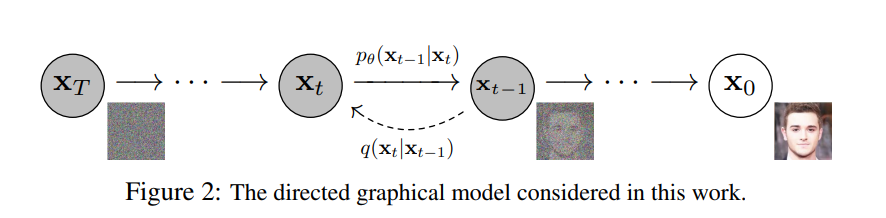
        不同于GAN，Diffusion基于噪声生成的图像和原图像是“同维度”的。

        相比起GAN，Diffusion算法的优点是什么呢？最大的优点是生成的图片质量要高的多！而且支持高像素图片的稳定生成。这一点是GAN无法企及的。此外Diffusion算法只需要训练“生成器”，不需要训练别的网络*（判别器等）*，这也导致在训练的难度上扩散算法要容易许多，不需要像GAN一样去做诸多的调参等等。这或许也验证了一句话：“几行简单正确的数学推导，可以比近十年的大规模调试超参调试网络结构有效得多。”

        Diffusion算法的问题也相当明显，最大的缺点就是训练开销特别大。扩散模型依赖于扩散步骤的长马尔可夫链来生成样本，因此在时间和计算方面会非常昂贵，尤其是对显存的要求非常高。

        我自己搭建的Stable-Diffusion模型，光是使用开源的、已经训练好的模型进行图片生成，都需要12G以上显存的显卡，而且图片的像素必须限制在1024*1024以下，不然就会爆显存。显存更小的显卡，可以生成的图片像素自然会更小，至于训练的开销就更不用说了。在这一点上，GAN具备了无可比拟的优势。也正因成本上的优势，GAN的灵活性目前要高得多。

2.1.7 GAN总结#

一、特点

• 无监督学习的方式，采用博弈论的思想，用对抗的方式生成图片

• GAN的思想很简单，因此部署起来非常方便，可以根据具体问题来灵活地构建

• GAN可以用于样本生成、AI换脸等等一系列和“生成样本”或者“图像”相关的任务

二、不足

• GAN的训练非常困难，如果判别器太强了，生成器的效果就会大打折扣，甚至梯度消失；如果判别器太弱了，生成器的梯度不准，图像会非常奇怪。只有判别器和生成器旗鼓相当，或者说不好不坏的时候，GAN的效果才会比较好。

• GAN比较适合一些比较小的图像生成，比如人脸、小的样本…对于比较大的图，训练难度会几何倍增长（分布计算难度增大）

• GAN的loss函数难以指引训练步骤，而对于判别器的判别操作，也有诸多的不足和优化的余地 (KL散度、JS散度、WGAN…)