一、论文概述# 本文是 f − d p f-dp f − d p μ − G D P \mu-GDP μ − G D P M o m e n t A c c o u n t a n t Moment Accountant M o m e n t A cco u n t an t R e n y i A c c o u n t a n t Renyi Accountant R e n y i A cco u n t an t μ − G D P \mu-GDP μ − G D P
这篇笔记主要关注的点在于:
μ − G D P \mu-GDP μ − G D P
μ − G D P \mu-GDP μ − G D P ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P
μ − G D P \mu-GDP μ − G D P ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P
二、f − D P f-DP f − D P # 这一部分主要关注 f-dp 在实际的模型构件中,主要运用到了哪些性质和知识点。简单来说,主要包括了以下这几点:
f − D P f-DP f − D P T ( M ( S ) , M ( S ’ ) ) ≥ f T(M(S),M(S’))\geq f T ( M ( S ) , M ( S ’ )) ≥ f 其中: T ( P , Q ) = i n f Φ { β Φ : α Φ ≤ α } 其中:T(P,Q)=inf_{\Phi}\{\beta_\Phi:\alpha_\Phi\leq \alpha\} 其中: T ( P , Q ) = in f Φ { β Φ : α Φ ≤ α }
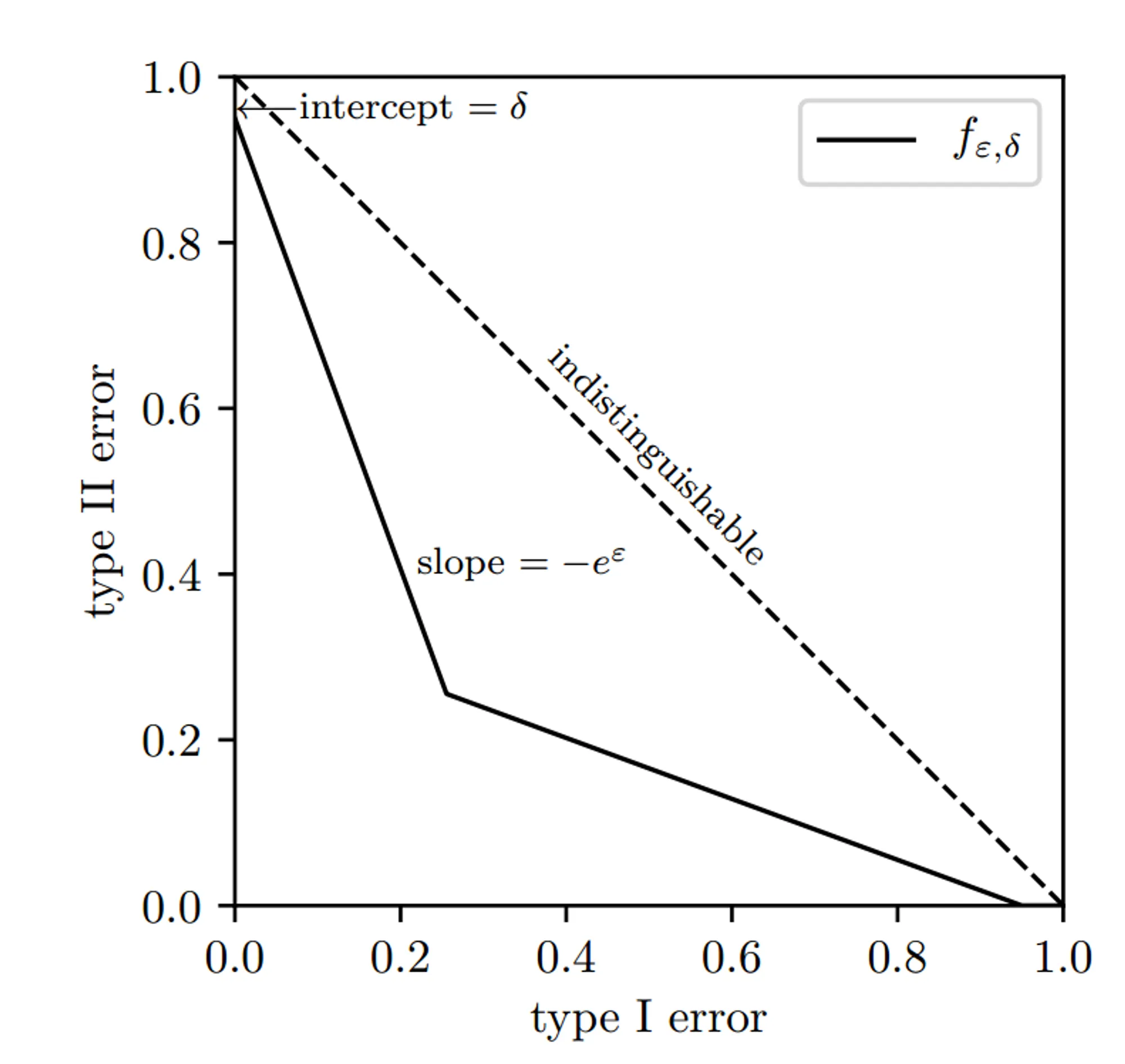
f − D P f-DP f − D P ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P f ϵ , δ ( α ) = m a x 0 , 1 − δ − e ϵ α , e − ϵ ( 1 − δ − α ) f_{\epsilon,\delta}(\alpha)=max{0,1-\delta-e^\epsilon\alpha,e^{-\epsilon}(1-\delta-\alpha)} f ϵ , δ ( α ) = ma x 0 , 1 − δ − e ϵ α , e − ϵ ( 1 − δ − α )
μ − G D P \mu-GDP μ − G D P
T(M(S),M(S’))\geq G_\mu$
μ − G D P \mu-GDP μ − G D P N ( 0 , σ 2 ) , 其中: σ = s e n s ( θ ) / μ , w i t h s e n s ( θ ) = s u p S , S ’ ∣ θ ( S ) − θ ( S ’ ) ∣ N(0, \sigma^2),其中:\sigma=sens(\theta)/\mu,\;\; with \;sens(\theta)=sup_{S,S’}|\theta(S)-\theta(S’)| N ( 0 , σ 2 ) , 其中: σ = se n s ( θ ) / μ , w i t h se n s ( θ ) = s u p S , S ’ ∣ θ ( S ) − θ ( S ’ ) ∣
组合机制和中心极限定理:f 1 ⊗ f 2 … ⊗ f T → G μ f_1 \otimes f_2…\otimes f_T \rightarrow G_\mu f 1 ⊗ f 2 … ⊗ f T → G μ μ \mu μ
对称性和优化:权衡函数采用 m i n { f p f p − 1 } min\{f_p\, f_p^{-1}\} min { f p f p − 1 }
三、算法和隐私分析# 3.1 Noisy SGD# 令 θ \theta θ l ( θ , x ) l(\theta,x) l ( θ , x ) t t t I t I_t I t p p p 1 , 2 , … , n {1,2,…,n} 1 , 2 , … , n b a t c h batch ba t c h p n pn p n
θ t + 1 = θ t − η t ⋅ 1 I t ∑ i ∈ I t ∇ θ l ( θ t , x i ) \theta_{t+1}=\theta_t-\eta_t·\frac{1}{I_t}\sum_{i\in I_t}\nabla_\theta l(\theta_t,x_i) θ t + 1 = θ t − η t ⋅ I t 1 i ∈ I t ∑ ∇ θ l ( θ t , x i ) 接下来对一些参数进行说明:
算法的步骤中,首先要对梯度进行裁剪,然后再往裁剪的梯度上添加高斯噪声,相当于对更新后的迭代应用高斯机制。这个步骤将梯度的更新范围限定在了 R 以内,因而灵敏度为 R。
添加的噪声为 σ R ⋅ N ( 0 , I ) \sigma R · N(0,I) σ R ⋅ N ( 0 , I ) N ( 0 , ( σ R ) 2 I ) N(0,(\sigma R)^2 I) N ( 0 , ( σ R ) 2 I ) 上篇文章的 4-3 处的描述 ,机制 M 符合 。
noisySGD 符合 m i n { f , f − 1 } ∗ ∗ − D P min\{f,f^{-1}\}^{**}-DP min { f , f − 1 } ∗∗ − D P f = ( p G 1 / σ + ( 1 − p ) I d ) ⊗ T f=(pG_{1/\sigma}+(1-p)Id)^{\otimes T} f = ( p G 1/ σ + ( 1 − p ) I d ) ⊗ T μ − G D P \mu-GDP μ − G D P
f = ( p G 1 / σ + ( 1 − p ) I d ) ⊗ T → G μ f=(pG_{1/\sigma}+(1-p)Id)^{\otimes T}\rightarrow G_\mu f = ( p G 1/ σ + ( 1 − p ) I d ) ⊗ T → G μ 当 T → ∞ T \rightarrow \infin T → ∞ p T → ν , p\sqrt{T} \rightarrow \nu, p T → ν , μ = ν e 1 / σ 2 − 1 \mu = \nu\sqrt{e^{1/\sigma^2}-1} μ = ν e 1/ σ 2 − 1
m i n { f , f − 1 } ∗ ∗ → m i n { G μ , G μ − 1 } ∗ ∗ = G μ ∗ ∗ = G μ min\{f,f^{-1}\}^{**}\rightarrow min\{G_\mu,G\mu^{-1}\}^{**}=G_\mu^{**}=G_\mu min { f , f − 1 } ∗∗ → min { G μ , G μ − 1 } ∗∗ = G μ ∗∗ = G μ 根据 p = B n p = \frac{B}{n} p = n B B n T ( e 1 / σ 2 − 1 ) \frac{B}{n}\sqrt{T(e^{1/\sigma^2}-1)} n B T ( e 1/ σ 2 − 1 )
算法如下所示:
Algorithm 1 NoisySGD
Input: Dataset S = { x 1 , … , x n } S = \{ x_1,…,x_n \} S = { x 1 , … , x n } l { θ , x } l\{\theta, x\} l { θ , x }
Parameters:
- initial weights θ 0 \theta_0 θ 0
- learning rate η t \eta_t η t
- subsampling probability p,
- number of iterations T,
- noise scale σ \sigma σ
- gradient norm bound R.
for t = 0 , … , T − 1 t = 0,…,T-1 t = 0 , … , T − 1 - Take a Poisson subsample I t ⊂ { 1 , … , n } I_t \subset \{1,…,n\} I t ⊂ { 1 , … , n }
- for i ∈ T t i \in T_t i ∈ T t
- ν t ( i ) ← ∇ θ l ( θ t , x i ) \nu_t^{(i)} \leftarrow \nabla_\theta l(\theta_t,x_i) ν t ( i ) ← ∇ θ l ( θ t , x i )
- ν ‾ t ( i ) ← ν t i / m a x { 1 , ∣ ∣ ν t ( i ) ∣ ∣ 2 / R } \overline{\nu}_t^{(i)} \leftarrow \nu _{t}^{i}/max\{ 1, ||\nu _t^{(i)}||_2/R \} ν t ( i ) ← ν t i / ma x { 1 , ∣∣ ν t ( i ) ∣ ∣ 2 / R }
- θ t + 1 ← θ t − η t ⋅ 1 ∣ I t ∣ ( ∑ i ∈ I t ν ‾ t ( i ) + σ R ⋅ N ( 0 , I ) ) \theta_{t+1}\leftarrow \theta_t-\eta_t·\frac{1}{|I_t|}(\sum_{i\in I_t}\overline{\nu}_t^{(i)}+\sigma R·N(0,I)) θ t + 1 ← θ t − η t ⋅ ∣ I t ∣ 1 ( ∑ i ∈ I t ν t ( i ) + σ R ⋅ N ( 0 , I ))
3.2 和 Moment Accountant 的比较# 首先证明如下的引理:
当 T → ∞ T \rightarrow \infin T → ∞ p T p\sqrt{T} p T
lim T → ∞ sup ( sup ϵ ≥ 0 f ϵ , δ M A ( ϵ ) ( α ) − G μ C L T ( α ) ) ≤ 0 \lim _{T\rightarrow \infin}\sup(\sup_{\epsilon \geq 0}f_{\epsilon, \delta_{MA}(\epsilon)}(\alpha)-G_{\mu_{CLT}}(\alpha))\leq0 T → ∞ lim sup ( ϵ ≥ 0 sup f ϵ , δ M A ( ϵ ) ( α ) − G μ C L T ( α )) ≤ 0 这里需要强调的一点是,在 ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P ϵ \epsilon ϵ f − d p f-dp f − d p f f f μ − G D P \mu-GDP μ − G D P μ \mu μ
实线部分为等效的 ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P δ \delta δ ϵ \epsilon ϵ ϵ \epsilon ϵ δ \delta δ ϵ \epsilon ϵ
f − d p f-dp f − d p
μ − G D P \mu-GDP μ − G D P T ( N ( 0 , 1 ) , N ( μ , 1 ) ) T(N(0,1),N(\mu,1)) T ( N ( 0 , 1 ) , N ( μ , 1 )) μ \mu μ
在上面的引理中涉及到了 ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P μ − G D P \mu-GDP μ − G D P μ − G D P \mu-GDP μ − G D P ( ϵ , δ ( ϵ ; μ ) ) − D P (\epsilon,\delta(\epsilon;\mu))-DP ( ϵ , δ ( ϵ ; μ )) − D P
δ ( ϵ ; μ ) = 1 + G μ ∗ ( − e ϵ ) = Φ ( − ϵ μ + μ 2 ) − e ϵ Φ ( − ϵ μ − μ 2 ) \delta(\epsilon;\mu)=1+G_\mu^*(-e^\epsilon)=\Phi(-\frac{\epsilon}{\mu}+\frac{\mu}{2})-e^\epsilon\Phi(-\frac{\epsilon}{\mu}-\frac{\mu}{2}) δ ( ϵ ; μ ) = 1 + G μ ∗ ( − e ϵ ) = Φ ( − μ ϵ + 2 μ ) − e ϵ Φ ( − μ ϵ − 2 μ ) 通过这个式子,我们可以把 μ − G D P \mu-GDP μ − G D P ( ϵ , δ ) − D P (\epsilon,\delta)-DP ( ϵ , δ ) − D P ϵ \epsilon ϵ δ \delta δ
一般来讲,我们有:
lim T → ∞ s u p ( δ C L T ( ϵ ) − δ M A ( ϵ ) ) < 0 , f o r a l l ϵ > 0 lim T → ∞ s u p ( ϵ C L T ( δ ) − ϵ M A ( δ ) ) < 0 , f o r a n t δ \lim_{T\rightarrow \infin} sup(\delta_{CLT}(\epsilon)-\delta_{MA}(\epsilon))<0,\;for\;all\;\epsilon\;>0\\ \lim_{T\rightarrow \infin}sup(\epsilon_{CLT}(\delta)-\epsilon_{MA}(\delta))<0,\;for\;ant\;\delta \;\;\;\;\;\; T → ∞ lim s u p ( δ C L T ( ϵ ) − δ M A ( ϵ )) < 0 , f or a ll ϵ > 0 T → ∞ lim s u p ( ϵ C L T ( δ ) − ϵ M A ( δ )) < 0 , f or an t δ 当然,我们也可以反过来,通过上面的式子,给定 ϵ \epsilon ϵ δ \delta δ μ \mu μ μ − G D P \mu-GDP μ − G D P
四、相关的推理证明# 4.1 邻近数据集的分辨难度# 【论点】:如果机制 M 是 f − D P f-DP f − D P S ‘ = S ∪ x 0 S‘ = S \cup {x_0} S ‘ = S ∪ x 0
T ( M ) ∘ S a m p l e p ( S ) , M ∘ S a m p l e p ( S ′ ) ) ≥ p f + ( 1 − p ) I d T(M) \circ Sample_p(S),M\circ Sample_p(S'))\geq pf+(1-p)Id T ( M ) ∘ S am pl e p ( S ) , M ∘ S am pl e p ( S ′ )) ≥ p f + ( 1 − p ) I d 【证明】:我们可以用一个向量 b ⃗ = ( b 1 , … , b n ) ∈ { 0 , 1 } n \vec{b}=(b_1,…,b_n)\in \{0,1\}^n b = ( b 1 , … , b n ) ∈ { 0 , 1 } n S b ⃗ ⊂ S S_{\vec{b}}\subset S S b ⊂ S b i b_i b i S a m p l e ( S ) Sample(S) S am pl e ( S ) S b ⃗ S_{\vec{b}} S b θ b ⃗ \theta_{\vec{b}} θ b b ⃗ \vec{b} b b ⃗ \vec{b} b θ b ⃗ = p k ( 1 − p ) n − k \theta_{\vec{b}} = p^k(1-p)^{n-k} θ b = p k ( 1 − p ) n − k
M ∘ S a m p l e p ( S ) = ∑ b ⃗ ∈ { 0 , 1 } n θ b ⃗ ⋅ M ( S b ⃗ ) M \circ Sample_p(S)=\sum_{\vec{b}\in\{0,1\}^n}\theta_{\vec{b}}·M(S_{\vec{b}}) M ∘ S am pl e p ( S ) = b ∈ { 0 , 1 } n ∑ θ b ⋅ M ( S b ) 同理,对于其邻近的数据集 S ′ = S ∪ x 0 S' = S\cup x_0 S ′ = S ∪ x 0 x 0 x_0 x 0 x 0 x_0 x 0
M ∘ S a m p l e p ( S ′ ) = ∑ b ⃗ ∈ { 0 , 1 } n p ⋅ θ b ⃗ ⋅ M ( S b ⃗ ∪ { x ) } ) + ∑ b ⃗ { 0 , 1 } n ( 1 − p ) ⋅ θ b ⃗ ⋅ M ( S b ⃗ ) M\circ Sample_p(S')=\sum_{\vec{b}\in \{0,1\}^n}p·\theta_{\vec{b}}·M(S_{\vec{b}}\cup\{x_)\})+\sum_{\vec{b}\{0,1\}^n}(1-p)·\theta_{\vec{b}}·M(S_{\vec{b}}) M ∘ S am pl e p ( S ′ ) = b ∈ { 0 , 1 } n ∑ p ⋅ θ b ⋅ M ( S b ∪ { x ) }) + b { 0 , 1 } n ∑ ( 1 − p ) ⋅ θ b ⋅ M ( S b ) 接下来我们借助一个引理,来证明该式子:
【引理】令 I I I i ∈ I i \in I i ∈ I P i P_i P i Q i Q_i Q i ( θ i ) i ∈ I (\theta_i)_{i\in I} ( θ i ) i ∈ I T ( P i , Q i ) ≥ f T(P_i,Q_i)\geq f T ( P i , Q i ) ≥ f
T ( ∑ θ i P i , ( 1 − p ) ∑ θ i P i + p ∑ θ i Q i ) ≥ p f + ( 1 − p ) I d T(\sum \theta_iP_i,(1-p)\sum\theta_iP_i+p\sum\theta_iQ_i)\geq pf+(1-p)Id T ( ∑ θ i P i , ( 1 − p ) ∑ θ i P i + p ∑ θ i Q i ) ≥ p f + ( 1 − p ) I d 如果该引理成立,那么自然令 b ⃗ ∈ { 0 , 1 } n \vec{b}\in\{0,1\}^n b ∈ { 0 , 1 } n P i P_i P i M ( S b ⃗ ) M(S_{\vec{b}}) M ( S b ) Q i Q_i Q i M ( S b ⃗ ∪ { x 0 } ) M(S_{\vec{b}}\cup\{x_0\}) M ( S b ∪ { x 0 }) T ( P i , Q i ) ≥ f T(P_i,Q_i)\geq f T ( P i , Q i ) ≥ f f − D P f-DP f − D P
【引理的证明】令 P = ∑ θ i P i P = \sum \theta_i P_i P = ∑ θ i P i Q = ( 1 − p ) ∑ θ i P i + p ∑ θ i Q i Q=(1-p)\sum\theta_i P_i+p\sum\theta_i Q_i Q = ( 1 − p ) ∑ θ i P i + p ∑ θ i Q i Φ \Phi Φ E P Φ = α E_P\Phi=\alpha E P Φ = α
T ( M ) ∘ S a m p l e p ( S ) , M ∘ S a m p l e p ( S ′ ) ) ≥ p f + ( 1 − p ) I d T(M) \circ Sample_p(S),M\circ Sample_p(S'))\geq pf+(1-p)Id T ( M ) ∘ S am pl e p ( S ) , M ∘ S am pl e p ( S ′ )) ≥ p f + ( 1 − p ) I d ∑ θ i E P i Φ = α \sum\theta_iE_{P_i}\Phi=\alpha ∑ θ i E P i Φ = α 那么 Q 便可以写成:
E Q Φ = ( 1 − p ) α + p ∑ θ i E Q i Φ E_{Q}\Phi = (1-p)\alpha+p\sum\theta_iE_{Q_i}\Phi E Q Φ = ( 1 − p ) α + p ∑ θ i E Q i Φ 根据定义,T ( P i , Q i ) ≥ f T(P_i,Q_i)\geq f T ( P i , Q i ) ≥ f T ( P i , Q i ) ( α ) = i n f { β Φ : α Φ ≤ α } T(P_i,Q_i)(\alpha)=inf\{\beta_\Phi:\alpha_\Phi\leq\alpha\} T ( P i , Q i ) ( α ) = in f { β Φ : α Φ ≤ α } β Φ = 1 − E Q [ Φ ] \beta_\Phi=1-E_Q[\Phi] β Φ = 1 − E Q [ Φ ] E Q i Φ ≤ 1 − f ( E P i Φ ) E_{Q_i}\Phi \leq 1-f(E_{P_i}\Phi) E Q i Φ ≤ 1 − f ( E P i Φ )
∑ θ i E Q i Φ ≤ 1 − ∑ θ i f ( E P i Φ ) \sum\theta_iE_{Q_i}\Phi\leq1-\sum\theta_if(E_{P_i}\Phi) ∑ θ i E Q i Φ ≤ 1 − ∑ θ i f ( E P i Φ ) 根据琴生不等式,对于属于凸函数的trade-off函数,有:
∑ θ i f ( E p I Φ ) ≥ f ( ∑ θ i E P i Φ ) = f ( α ) \sum\theta_if(E_{p_I}\Phi)\geq f(\sum \theta_iE_{P_i}\Phi)=f(\alpha) ∑ θ i f ( E p I Φ ) ≥ f ( ∑ θ i E P i Φ ) = f ( α ) 则:
E Q Φ ≤ ( 1 − p ) α + p ( 1 − ∑ θ i f ( E P i Φ ) ) ≤ ( 1 − p ) α + p ( 1 − f ( α ) ) E_{Q}\Phi\leq(1-p)\alpha+p(1-\sum\theta_if(E_{P_i}\Phi))\leq(1-p)\alpha+p(1-f(\alpha)) E Q Φ ≤ ( 1 − p ) α + p ( 1 − ∑ θ i f ( E P i Φ )) ≤ ( 1 − p ) α + p ( 1 − f ( α )) 根据定义,T ( P i , Q i ) ( α ) = i n f { β Φ : α Φ ≤ α } T(P_i,Q_i)(\alpha)=inf\{\beta_\Phi:\alpha_\Phi\leq\alpha\} T ( P i , Q i ) ( α ) = in f { β Φ : α Φ ≤ α } β Φ = 1 − E Q [ Φ ] \beta_\Phi=1-E_Q[\Phi] β Φ = 1 − E Q [ Φ ] E Q [ Φ ] E_Q[\Phi] E Q [ Φ ] β Φ \beta_\Phi β Φ E Q [ Φ ] E_Q[\Phi] E Q [ Φ ] ( 1 − p ) α + p ( 1 − f ( α ) ) (1-p)\alpha+p(1-f(\alpha)) ( 1 − p ) α + p ( 1 − f ( α ))
T ( P i , Q i ) ( α ) ≥ 1 − ( 1 − p ) α − p ( 1 − f ( α ) ) = ( 1 − p ) ( 1 − α ) + p f T(P_i,Q_i)(\alpha)\geq1-(1-p)\alpha-p(1-f(\alpha))=(1-p)(1-\alpha)+pf T ( P i , Q i ) ( α ) ≥ 1 − ( 1 − p ) α − p ( 1 − f ( α )) = ( 1 − p ) ( 1 − α ) + p f 又有 1 − α = I d 1-\alpha = Id 1 − α = I d
T ( ∑ θ i P i , ( 1 − p ) ∑ θ i P i + p ∑ θ i Q i ) ≥ p f + ( 1 − p ) I d T(\sum \theta_iP_i,(1-p)\sum\theta_iP_i+p\sum\theta_iQ_i)\geq pf+(1-p)Id T ( ∑ θ i P i , ( 1 − p ) ∑ θ i P i + p ∑ θ i Q i ) ≥ p f + ( 1 − p ) I d 引理证毕!这个式子说明了子采样会如何影响最终的隐私保护(子采样在这个式子里以 p 的方式呈现)。
4.2 NoisySGD 隐私分析# 【结论】算法符合 { f , f − 1 } ∗ ∗ − D P \{f,f^{-1}\}^{**}-DP { f , f − 1 } ∗∗ − D P
f = ( p G 1 / σ + ( 1 − p ) I d ) ⊗ T f=(pG_{1/\sigma}+(1-p)Id)^{\otimes T} f = ( p G 1/ σ + ( 1 − p ) I d ) ⊗ T 【证明】首先,根据原 Gasussian Differential Privacy 的论文,我们可以得到如下的一个引理:
【引理】假设 M 1 : X → Y , M 2 : X × Y → Z M_1:X\rightarrow Y, M_2:X\times Y\rightarrow Z M 1 : X → Y , M 2 : X × Y → Z S S S S ′ = S ∪ { x 0 } S'=S\cup \{x_0\} S ′ = S ∪ { x 0 }
T ( M 1 ( S ) , M ( S ’ ) ) ≥ f T(M_1(S),M(S’))\geq f T ( M 1 ( S ) , M ( S ’ )) ≥ f
T ( M 2 ( S , y ) , M 2 ( S ’ , y ) ) ≥ g , f o r a n y y ∈ Y T(M_2(S,y), M_2(S’,y))\geq g, \;for\;any\;y\;\in Y T ( M 2 ( S , y ) , M 2 ( S ’ , y )) ≥ g , f or an y y ∈ Y
那么,对于组合 M 2 ∘ M 1 M_2\circ M_1 M 2 ∘ M 1 X → Y × Z X\rightarrow Y\times Z X → Y × Z
T ( M 2 ∘ M 1 ( S ) , M 2 ∘ M 1 ( S ′ ) ) ≥ f ⊗ g T(M_2\circ M_1(S),M_2\circ M_1(S'))\geq f\otimes g T ( M 2 ∘ M 1 ( S ) , M 2 ∘ M 1 ( S ′ )) ≥ f ⊗ g 继续上面的证明:
由 4.1 的分析证明,NoisySGD 算法可以理解为:
N o i s y S G D : X n → V × V . . . V S → ( θ 1 , θ 2 . . . , θ T ) NoisySGD:X^n\rightarrow V\times V...V\\ S\rightarrow (\theta_1,\theta_2...,\theta_T) N o i sy SG D : X n → V × V ... V S → ( θ 1 , θ 2 ... , θ T ) 上述的这个过程,就是 T 个 M 机制的组合。因此有:
T ( N o i s y S G D ( S ) , N o i s y S G D ( S ′ ) ) ≥ ( p G 1 / σ + ( 1 − p ) I d ) ⊗ T = f T(NoisySGD(S),NoisySGD(S'))\geq(pG_{1/\sigma}+(1-p)Id)^{\otimes T}=f T ( N o i sy SG D ( S ) , N o i sy SG D ( S ′ )) ≥ ( p G 1/ σ + ( 1 − p ) I d ) ⊗ T = f 需要注意的是,T ( N o i s y S G D ( S ) , N o i s y S G D ( S ′ ) ) ≥ f − 1 T(NoisySGD(S),NoisySGD(S'))\geq f^{-1} T ( N o i sy SG D ( S ) , N o i sy SG D ( S ′ )) ≥ f − 1
我们可以从这两个关系里得出:S 和 S‘ 的权衡函数的下界必然是 f f f f − 1 f^{-1} f − 1 { f , f − 1 } ∗ ∗ − D P \{f,f^{-1}\}^{**}-DP { f , f − 1 } ∗∗ − D P